
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача К1
Задача К1
Точка В движется в плоскости xy (табл. К1.1, К1.2). Закон движения точки задан уравнениями: x=f1( t ), y=f2( t ), где x и y выражены в сантиметрах, t - в секундах.
Найти уравнение траектории точки; для момента времени t1=1c определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Зависимость x=f1( t ) указана в табл. К1.1, а зависимость y=f2(t) дана в табл. К1.2 (для вар.0 - 2 в столбце 2, для вар.3 - 6 в столбце 3, для вар.7 - 9 в столбце 4). Номер варианта в табл. К1.1 выбирается по предпоследней цифре шифра, а номер условия в табл. К1.2 - по последней.
Указания. Задача К1 относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение
точки в декартовых координатах ( координатный способ задания движения точки ), а также формул, по которым определяются касательное и нормальное ускорения точки.
В данной задаче все искомые величины нужно определить только для момента времени t1=1с.
Таблица К1.1
| № вар. | x = f (t) | № вар. | x = f (t) |
| x = 4 sin (pt/2) | x = 2t | ||
| x = 3 - 6 sin (pt/2) | x = 2t + 2 | ||
| x = 3 sin (pt/2) - 2 | x = 12 cos (pt/2) | ||
| x = 4 - 2t | x = 6 cos (pt/2) - 2 | ||
| x = 2t + 4 | x = 4 - 8 cos (pt/2) |
Таблица К1.2
| Номер | y = f2 ( t ) | ||
| условия | Вар. 0 - 2 | Вар. 3 - 6 | Вар. 7 - 9 |
| 9cos(pt/2) | t2 - 2 | -4cos(pt/2) | |
| 3cos(pt/2) | (t + 4)2 | 10sin(pt/2) | |
| 6cos2(pt/2) | 4 + 2t2 | 12sin2(pt/2) | |
| 12cos(pt/2) | 2(t + 1)2 | 4sin(pt/2) | |
| 9cos(pt/2) | 4t2 - 2 | 12cos(pt/2) | |
| -10cos(pt/2) | 3t2 - 2 | 3sin(pt/2) | |
| 8cos(pt/2) | (t + 1)3 | 16sin2(pt/2) | |
| -9cos2(pt/2) | 6t2 | 6cos(pt/2) | |
| 6cos(pt/2) | 2t3 | - 9sin(pt/2) | |
| 2cos(pt/2) | 4t3 | 8cos(pt/2) |
Пример К1. Даны уравнения движения точки в плоскости ху :
x = 2 t , y = t2 (1)
(х, у - в сантиметрах, t - в секундах).
Определить уравнение траектории точки; для момента времени t1 = 1 c найти скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Решение. Для определения уравнения траектории точки исключим из заданных уравнений движения время t.
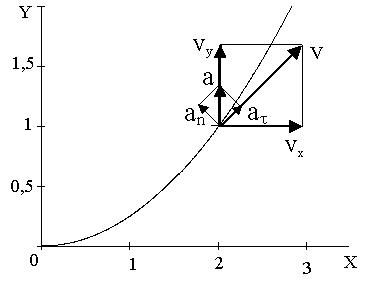
Отсюда находим следующее уравнение траектории точки (парабола, рис. К1):
y = x2 / 4 (2)
Скорость точки найдем по ее проекциям на координатные оси:

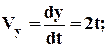
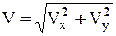
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|