Задача С1

Задача С1

Жесткая рама (рис. С1.0 - С1.9, табл. С1) закреплена в точке А шарнирно, а в точке В прикреплена к шарнирной опоре на катках.

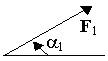
На раму действуют пара сил с моментом М=100 Н×м и сила, значение, направление и точка приложения которой указаны в таблице (например, в условиях № 1 на раму действует сила F₁ = 10 Н под углом 30° к горизонтальной оси, приложенная в точке К).

Определить реакции связей в точках А и В, вызываемые заданными нагрузками. При окончательных подсчетах принять L=0,5 м.

Указания. Задача С1 - на равновесие тела под действием плоской системы сил. Составляя уравнения равновесия, учесть, что уравнение моментов будет более простым (содержать меньше неизвестных),

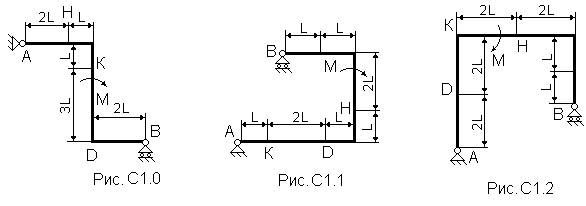
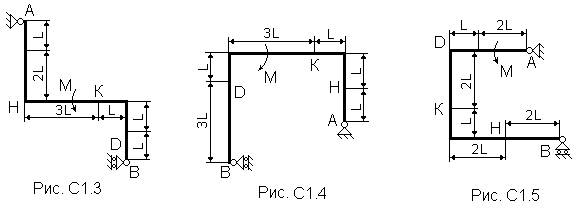
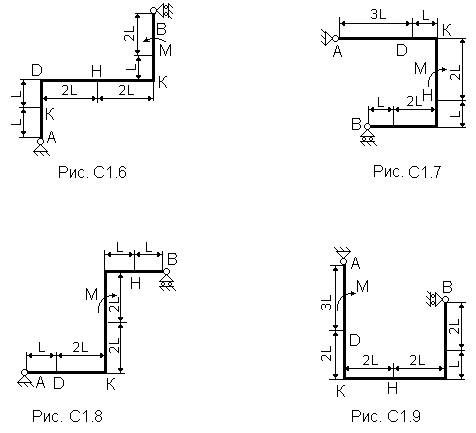
Таблица С1

Сила
	F₁=10 H		F₂=20 H		F₃=30 H		F₄=40 H
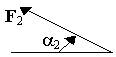
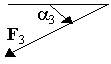
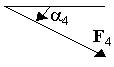
Номер условия	Точка прилож.	a°₁	Точка прилож.	a°₂	Точка прилож.	a°₃	Точка прилож.	a°₄
	-	-	D				-	-
	К		-	-	-	-
	-	-			K		-	-
			-	-	-	-	D
	-	-			D		-	-
	H		-	-			-	-
	-	-			-	-	K
	D		-	-			-	-
	-	-	H		-	-
			-	-	-	-	K

если брать моменты относительно точки, где пересекаются линии действия двух реакций связей (в данном случае относительно точки B). При вычислении момента силы F часто удобно разложить ее на составляющие F^/ и F^//, для которых плечи легко вычисляются, в частности на составляющие, параллельные координатным осям, и воспользоваться теоремой Вариньона; тогда m_O(F)=m₀(F^/)+m₀(F^//).

Пример С1. Жесткая рама АВС ( рис. С1 ) имеет в точке B неподвижную шарнирную опору, а в точке C - подвижную шарнирную опору на катках. Все действующие нагрузки и размеры показаны на рисунке.

Рис. С1

Дано: F=25 кH, a=60^o, b=30°, М=50 кH×м, L=0,5 м.

Определить: реакции в точках B и C, вызываемые действующими нагрузками.

Решение. Рассмотрим равновесие рамы. Проведем координатные оси ХУ и изобразим действующие на раму силы: силу F, пару сил с моментом М и реакции связей X_B, Y_B, R_C (реакцию неподвижной шарнирной опоры B изображаем двумя ее составляющими, реакция шарнирной опоры на катках направлена перпендикулярно опорной плоскости).

Составим три уравнения равновесия плоской системы сил. При вычислении момента силы F относительно точки B воспользуемся теоремой Вариньона, т.е. разложим силу F на составляющие F^’, F’’ (F^’=Fcos a, F^’’=Fsin a) и учтем, что m_B(F)=m_B(F^’)+m_B(F^''). Получим :

1. SF_kx = 0, X_B + R_C sinb - F cosa = 0;

2. SF_ky = 0, У_B + R_C cosb + F sina = 0;

3. Sm_B(F_k) = 0, M - R_Ccosb×4L+ F cosa × 2L= 0.

Из этих уравнений находим:

Из (3):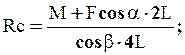

Из (1): X_B = - R_C sinb + F cosa;

Из (2): Y_B = - R_C cosb - F sina;

Подставив в составленные уравнения числовые значения заданных величин, и решив эти уравнения, определим искомые реакции.

Ответ: X_B= - 5,5 кH, Y_B= 9,6 кH, R_C=36,1 кH.

Знаки указывают, что сила X_B направлена противоположно показанной на рис.С1.

⇐ Предыдущая 123 4 5 Следующая ⇒