Напоминание. Эксцентриситет кривой второго порядка (конического сечения) – число, равное отношению расстояния от любой точки кривой 2-го порядка до фокуса к расстоянию от этой точки до соответствующей директрисы.

РИС. 3-13

2-ой закон Кеплера (1609 год)

В невозмущенном движении площадь, описываемая радиусом-вектором точки, движущейся в поле центральных сил, изменяется пропорционально времени.

Радиус-вектор планеты за равные промежутки времени описывает равные площади.

Оба эти закона Кеплера были в свое время получены в результате обработки экспериментальных данных Тихо Браге (1546-1601) и привели впоследствии Ньютона к установлению закона всемирного тяготения: 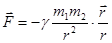- всегда притяжение – единственная сила, управляющая движением астрономических тел.

3-ий закон Кеплера (1619 год).

Формулировка Кеплера:

квадраты времен обращений планет относятся как кубы больших осей эллиптических орбит, по которым они движутся вокруг Солнца: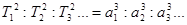

Справедливость 3-го закона Кеплера можно доказать, если считать орбиты планет круговыми. Это предположение не слишком грубое, так как эксцентриситет орбит планет невелик: для орбиты Земли »0.017, для орбиты Меркурия »0.205.

Напоминание

Эксцентриситет кривой второго порядка (конического сечения) – число, равное отношению расстояния от любой точки кривой 2-го порядка до фокуса к расстоянию от этой точки до соответствующей директрисы.

РИС. 3-14

У эллипса две директрисы ( ), каждая соответствует своему фокусу ; эксцентриситет: . Уравнение директрис: ; . Если , то и эллипс вырождается в прямую . Если , то директриса удаляется в бесконечность, фокусы сливаются в один. Эллипс превращается в окружность.

Итак, малость эксцентриситетов орбит планет Солнечной системы позволяет считать их орбиты круговыми.

Пусть одна планета имеет массу 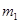, круговую орбиту радиуса 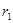и период обращения 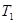, вторая планета - .

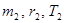Стационарное состояние: центробежная сила равна и противоположно направлена силе притяжения:

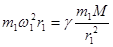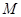, где - масса Солнца,

Гравитационная постоянная g =6,6710^-11 м³/кгс² или

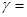(6.6732±0.0031)× 10^-8 дин×см²/г² [Н×м²/кг²].

- универсальная константа.

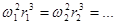Заменяя 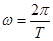, находим:

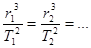или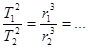

Для планет, движущихся по круговым орбитам, 3-ий закон Кеплера:

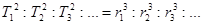
Мы знаем, что ускорение материальной точки (планеты) при равномерном движении по круговой орбите:

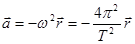. Подставим следующее обозначение: 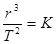(постоянная Кеплера); 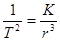; тогда 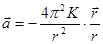и соответственно сила .

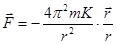Поскольку планета и Солнце равноправно должны входить в закон взаимодействия:

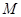, где - масса Солнца. Из сравнения сил видно, что

постоянная Кеплера .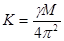

Ньютон не объяснил происхождения гравитационного взаимодействия – одной из фундаментальных сил природы. Общая теория относительности тоже не дает какого-либо наглядного толкования тяготения, дает лишь новый способ описания и более глубокое обобщение закона всемирного тяготения.

4 Лекция 4

⇐ Предыдущая 1 23