задача сводится к проблеме движения материальной точки в поле центральных сил.

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

Рис. 2-10

Работа силы 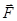на траектории 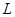между точками 1 и 2 равна сумме работ на элементарных отрезках:

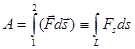
- криволинейный интеграл 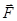по .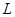

Конец Напоминания.

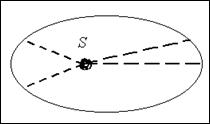
Проблема движения планет

Воспользуемся полученной информацией для рассмотрения проблемы движения планет Солнечной системы.

РИС. 3-11

Радиус орбиты движения Земли (T) вокруг Солнца (S) 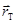»150000000 км.

Если пренебречь взаимодействием между планетами,

задача сводится к проблеме движения материальной точки в поле центральных сил.

Введем понятие секториальной скорости.

Пусть в момент времени t положение точки определяется радиусом-вектором 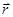, через промежуток времени 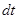- радиусом-вектором .

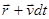РИС. 3-12

Величине 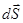придается векторный смысл, чтобы зафиксировать направление движения. Площадь, ометаемая радиусом-вектором точки, движущейся вокруг силового центра О, за время : .

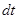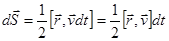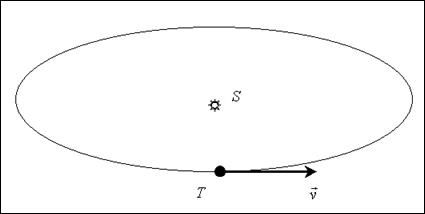
Скорость изменения площади, ометаемой радиусом-вектором (секториальная скорость): .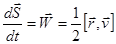

По определению момента количества движения .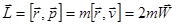

- в случае движения материальной точки в центральном поле ее момент количества движения пропорционален ее секториальной скорости.

Два следствия

1) Постоянство вектора – это постоянство не только его абсолютного значения (модуля), но и его направления. Значит, плоскость, перпендикулярная , занимает постоянное положение в пространстве; именно в этой плоскости лежат вектора 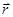и 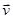. Следовательно, траектория движения материальной точки в поле центральных сил – это плоская кривая.

1-ый закон Кеплера(1609 год)

В невозмущенном движении, т.е. в задаче двух тел, орбита движущейся точки есть плоская кривая второго порядка, в одном из фокусов которой находится центр силы притяжения.

Планеты движутся вокруг Солнца по эллипсам, в одном из фокусов которых находится Солнце.

2) Из постоянства модуля вектора 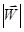следует, что в равные времена радиус-вектор материальной точки, движущейся в поле центральных сил, ометает равные площади.

⇐ Предыдущая 123 Следующая ⇒