b. Пример 12b

12.2.b. Пример 12b

Решить МКР пример 4. Сравнить с решением МКЭ. Построить график.

Программу для этого примера напишем на основе программы для примера 4 с использованием программы для примера 12a. Введём исходные данные и вычислим частные производные F_z, F_p, F_q.

clear all

format long

disp('Решаем пример 12b')

n = 20; % интервалов разбиения по меньшей стороне

syms x y z Dzx Dzy % описали переменные

F = Dzx^2-2*Dzy^2+2*y*z*(sin(pi*x)+x/5); % подынтегральная функция

zc = x/10+y^2/50; % функция граничных условий

x1 = 0;

x2 = 1;

y1 = 0;

y2 = 2;

fprintf('Подынтегральная функция: F=%s\n',char(F))

fprintf('Граничное условие на контуре: z=%s\n',char(zc))

fprintf('Область: %d<=x<=%d; %d<=y<=%d\n',x1,x2,y1,y2)

dFdz = diff(F,z);

dFdp = diff(F,Dzx);

dFdq = diff(F,Dzy);

Решаем пример 12b

Подынтегральная функция: F=Dzx^2-2*Dzy^2+2*y*z*(sin(pi*x)+1/5*x)

Граничное условие на контуре: z=1/10*x+1/50*y^2

Область: 0<=x<=1; 0<=y<=2

Строим квадратную сетку разбиения области.

del = min(x2-x1,y2-y1)/n % шаг сетки

nx = round((x2-x1)/del)

ny = round((y2-y1)/del)

del =

0.05000000000000

nx =

ny =

Описываем символические переменные: x, y, z в необходимых точках.

syms xim1 xi xip1 ykm1 yk ykp1 zim1km1 zim1k zim1kp1 zikm1 zik zikp1 zip1km1 zip1k zip1kp1

dx = sym((x2-x1)/nx)

dy = sym((y2-y1)/ny)

dx =

1/20

dy =

1/20

Формируем конечноразностное уравнение (12.5).

Zik = subs(dFdz,{x,y,z,Dzx,Dzy},{(xim1+xi)/2, (ykm1+yk)/2, (zik+zim1k+zikm1+zim1km1)/4,(zik-zim1k)/dx,(zik-zikm1)/dy});

Zip1k = subs ( dFdz, {x,y,z,Dzx,Dzy}, {(xi+xip1)/2, (ykm1+yk)/2, (zip1k+zik+zip1km1+zikm1)/4, (zip1k-zik)/dx, (zip1k-zip1km1)/dy});

Zikp1 = subs ( dFdz, {x,y,z,Dzx,Dzy}, {(xim1+xi)/2, (yk+ykp1)/2, (zikp1+zim1kp1+zik+zim1k)/4, (zikp1-zim1kp1)/dx, (zikp1-zik)/dy});

Zip1kp1 = subs ( dFdz, {x,y,z,Dzx,Dzy}, {(xi+xip1)/2, (yk+ykp1)/2 (zip1kp1+zikp1+zip1k+zik)/4, (zip1kp1-zikp1)/dx, (zip1kp1-zip1k)/dy});

Pik = subs ( dFdp, {x,y,z,Dzx,Dzy}, {(xim1+xi)/2, (ykm1+yk)/2, (zik+zim1k+zikm1+zim1km1)/4, (zik-zim1k)/dx, (zik-zikm1)/dy});

Pip1k = subs ( dFdp, {x,y,z,Dzx,Dzy}, {(xi+xip1)/2, (ykm1+yk)/2, (zip1k+zik+zip1km1+zikm1)/4, (zip1k-zik)/dx, (zip1k-zip1km1)/dy});

Qik = subs ( dFdq, {x,y,z,Dzx,Dzy}, {(xim1+xi)/2, (ykm1+yk)/2, (zik+zim1k+zikm1+zim1km1)/4, (zik-zim1k)/dx, (zik-zikm1)/dy});

Qikp1 = subs ( dFdq, {x,y,z,Dzx,Dzy}, {(xim1+xi)/2, (yk+ykp1)/2, (zikp1+zim1kp1+zik+zim1k)/4, (zikp1-zim1kp1)/dx, (zikp1-zik)/dy});

EqF = (Zik+Zip1k+Zikp1+Zip1kp1)/4 - (Pip1k-Pik)/dx - (Qikp1-Qik)/dy;

EqF = simple(EqF)

EqF =

1/4*(ykm1+yk)*(sin(pi*(1/2*xim1+1/2*xi))+1/10*xim1+1/10*xi)+1/4*(ykm1+yk)*(sin(pi*(1/2*xi+1/2*xip1))+1/10*xi+1/10*xip1)+1/4*(yk+ykp1)*(sin(pi*(1/2*xim1+1/2*xi))+1/10*xim1+1/10*xi)+1/4*(yk+ykp1)*(sin(pi*(1/2*xi+1/2*xip1))+1/10*xi+1/10*xip1)-800*zip1k-1600*zik-800*zim1k+1600*zikp1+1600*zikm1

Записываем функцию EqF в файл.

f{1} = 'function y = MyEqF ( xy, zim1km1, zikm1, zip1km1, zim1k, zik, zip1k, zim1kp1, zikp1, zip1kp1 )';

f{2} = 'xim1=xy(1); xi=xy(2); xip1=xy(3); ykm1=xy(4); yk=xy(5); ykp1=xy(6);';

f{3} = ['y=' char(EqF) ';' ]; % формируем функцию

disp('Текст файла MyEqF.m')

fprintf ( '%s\n', f{:} );

fid = fopen ( 'C:\Iglin\Matlab\MyEqF.m', 'w' );

fprintf ( fid, '%s\n', f{:} );

fclose(fid); % закрываем файл

Текст файла MyEqF.m

function y = MyEqF ( xy, zim1km1, zikm1, zip1km1, zim1k, zik, zip1k, zim1kp1, zikp1, zip1kp1 )

xim1=xy(1); xi=xy(2); xip1=xy(3); ykm1=xy(4); yk=xy(5); ykp1=xy(6);

y=1/4*(ykm1+yk)*(sin(pi*(1/2*xim1+1/2*xi))+1/10*xim1+1/10*xi)+1/4*(ykm1+yk)*(sin(pi*(1/2*xi+1/2*xip1))+1/10*xi+1/10*xip1)+1/4*(yk+ykp1)*(sin(pi*(1/2*xim1+1/2*xi))+1/10*xim1+1/10*xi)+1/4*(yk+ykp1)*(sin(pi*(1/2*xi+1/2*xip1))+1/10*xi+1/10*xip1)-800*zip1k-1600*zik-800*zim1k+1600*zikp1+1600*zikm1;

Формируем систему конечноразностных уравнений. Из-за большого размера системы уравнений применяем разрежённую матрицу. Нумеруем уравнения так, чтобы быстрее менялась координата y. Для каждого уравнения вычисляем входящие в него величины: правые части и коэффициенты при всех неизвестных. Заполняем матрицу коэффициентов и вектор правых частей. Если точка расположена на боковой стороне или в углу, учитываем граничное условие.

neq = (nx-1)*(ny-1) % число уравнений

A = sparse(neq,neq);

b = zeros(neq,1);

edx = eval(dx);

edy = eval(dy);

for i=1:nx-1,

xi = x1+i*edx;

xim1 = xi-edx;

xip1 = xi+edx;

for k=1:ny-1,

yk = y1+k*edy;

ykm1 = yk-edy;

ykp1 = yk+edy;

numeq = (i-1)*(ny-1)+k; % номер уравнения

xy = [xim1,xi,xip1,ykm1,yk,ykp1];

ei0 = MyEqF(xy,0,0,0,0,0,0,0,0,0);

eim1km1 = MyEqF(xy,1,0,0,0,0,0,0,0,0)-ei0;

eikm1 = MyEqF(xy,0,1,0,0,0,0,0,0,0)-ei0;

eip1km1 = MyEqF(xy,0,0,1,0,0,0,0,0,0)-ei0;

eim1k = MyEqF(xy,0,0,0,1,0,0,0,0,0)-ei0;

eik = MyEqF(xy,0,0,0,0,1,0,0,0,0)-ei0;

eip1k = MyEqF(xy,0,0,0,0,0,1,0,0,0)-ei0;

eim1kp1 = MyEqF(xy,0,0,0,0,0,0,1,0,0)-ei0;

eikp1 = MyEqF(xy,0,0,0,0,0,0,0,1,0)-ei0;

eip1kp1 = MyEqF(xy,0,0,0,0,0,0,0,0,1)-ei0;

b(numeq) = -ei0; % правая часть

A(numeq,numeq) = eik; % диаг. элемент (i,k)

if k<ny-1 % точки на серединах сторон

A(numeq,numeq+1) = eikp1; % (i,k+1)

else

b(numeq) = b(numeq)-eikp1*subs(zc,{x,y},{xi,ykp1});

end

if k>1

A(numeq,numeq-1) = eikm1; % (i,k-1)

else

b(numeq) = b(numeq)-eikm1*subs(zc,{x,y},{xi,ykm1});

end

if i<nx-1

A(numeq,numeq+ny-1) = eip1k; % (i+1,k)

else

b(numeq) = b(numeq)-eip1k*subs(zc,{x,y},{xip1,yk});

end

if i>1

A(numeq,numeq-ny+1) = eim1k; % (i-1,k)

else

b(numeq) = b(numeq)-eim1k*subs(zc,{x,y},{xim1,yk});

end

if (i<nx-1)&(k>1) % угловые точки

A(numeq,numeq+ny-2) = eip1km1; % (i+1,k-1)

else

b(numeq) = b(numeq) - eip1km1 * subs(zc,{x,y},{xip1,ykm1});

end

if (i<nx-1)&(k<ny-1)

A(numeq,numeq+ny) = eip1kp1; % (i+1,k+1)

else

b(numeq) = b(numeq) - eip1kp1 * subs(zc,{x,y},{xip1,ykp1});

end

if (i>1)&(k>1)

A(numeq,numeq-ny) = eim1km1; % (i-1,k-1)

else

b(numeq) = b(numeq) - eim1km1 * subs(zc,{x,y},{xim1,ykm1});

end

if (i>1)&(k<ny-1)

A(numeq,numeq-ny+2) = eim1kp1; % (i-1,k+1)

else

b(numeq) = b(numeq) - eim1kp1 * subs(zc,{x,y},{xim1,ykp1});

end

neq =

741

Решаем систему уравнений метода конечных разностей и преобразовываем вектор-столбец решений в двумерный массив нужной размерности. Строим массив увеличенных размеров, заполняем его крайние элементы граничными условиями, а средние – полученным решением. Формируем сетку (x,y), соответствующую полученному решению. Рисуем график в виде трёхмерной поверхности с затенением. Надписываем оси. Выравниваем масштабы по осям Ox и Oy. Выбираем палитру.

zeq = A\b; % решили СЛАУ

zsq = reshape(zeq,ny-1,nx-1); % переформатировали

zfull = zeros(ny+1,nx+1); % полная сетка нулей

[X,Y] = meshgrid(linspace(x1,x2,nx+1),linspace(y1,y2,ny+1));

zfull = subs(zc,{x,y},{X,Y}); % граничныые условия

zfull(2:ny,2:nx) = zsq; % решение

surfl(X,Y,zfull) % строим поверхность

title('\bfExample 12b')

xlabel('x')

ylabel('y')

zlabel('z(x,y)')

v = axis;

da = daspect;

da(1:2) = min(da(1:2));

daspect(da);

axis(v);

colormap(gray) % палитра

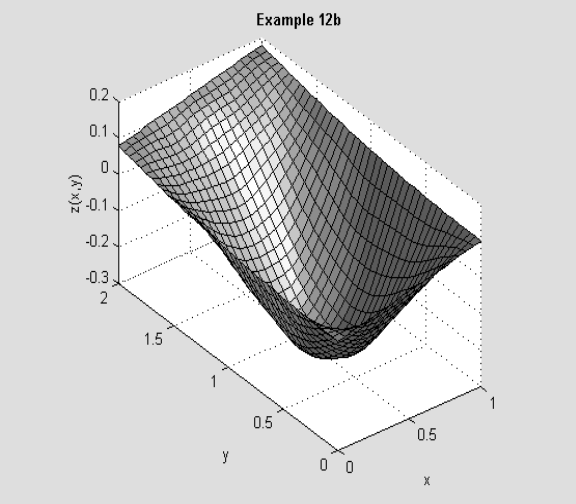
Рис. 12.2. Решение примера 12b

Ответ. Для сетки 20´40 система уравнений МКР вида (12.3) имеет вид

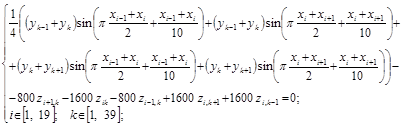(12.8)

при этом входящие в (12.8) величины z при i=1, i=20, k=1, k=40 находятся из граничного условия в соответствующей точке. График экстремальной поверхности показан на рисунке в зоне вывода. Видно, что он очень похож на поверхность, построенной по МКЭ в главе 4.

12.3. Задание

Решить примеры 1a и 4 методом конечных разностей. Сравнить решения с аналитическими.

⇐ Предыдущая 1 23