
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Примеры выполнения заданий. a. Пример 12a
12.2. Примеры выполнения заданий
12.2.a. Пример 12a
Решить методом конечных разностей пример 1a. Сравнить решение с аналитическим. Построить графики.
На основе программы для примера 1a составим программу для данного примера. Вводим исходные данные. Решаем пример 1a.
clear all
format long
disp('Решаем пример 12a')
nf = 10; % число интервалов разбиения
syms x y Dy D2y % описали символические переменные
F = x^2+y^2+Dy^2; % подынтегральная функция
x1 = -1;
y1 = 1;
x2 = 1;
y2 = 2;
fprintf('Подынтегральная функция: F=%s\n',char(F))
fprintf('Граничные условия: y(%d)=%d; y(%d)=%d\n',x1,y1,x2,y2)
dFdy = diff(F,y);
dFdy1 = diff(F,Dy);
d_dFdy1_dx = diff(dFdy1,x);
d_dFdy1_dy = diff(dFdy1,y);
d_dFdy1_dy1 = diff(dFdy1,Dy); % d(dF/dy')/dy'
dFy1dx = d_dFdy1_dx + d_dFdy1_dy*Dy + d_dFdy1_dy1*D2y;
Euler = simple(dFdy-dFy1dx);
deqEuler = [ char(Euler) '=0' ]; % составили уравнение
Sol = dsolve(deqEuler,'x'); % решаем уравнение Эйлера
if length(Sol)~=1 % решений нет или более одного
error('Нет решений или более одного решения!');
end
SolLeft = subs(Sol,x,sym(x1));
SolRight = subs(Sol,x,sym(x2));
EqLeft = [char(SolLeft) '=' char(sym(y1))];
EqRight = [char(SolRight) '=' char(sym(y2))];
Con = solve(EqLeft,EqRight); % решаем систему
C1 = Con.C1;
C2 = Con.C2;
Sol1a = vpa(eval(Sol),14);
xpl = linspace(x1,x2);
y1a = subs(Sol1a,x,xpl);
Решаем пример 12a
Подынтегральная функция: F=x^2+y^2+Dy^2
Граничные условия: y(-1)=1; y(1)=2
Формируем и печатаем конечноразностное уравнение (12.4).
syms xim1 xi xip1 yim1 yi yip1
dx = sym((x2-x1)/nf)
dFdyP = subs ( dFdy, {x,y,Dy}, {(xim1+xi)/2, (yim1+yi)/2, (yi-yim1)/dx});
dFdyN = subs ( dFdy, {x,y,Dy}, {(xi+xip1)/2,(yi+yip1)/2,(yip1-yi)/dx});
dFdy1P = subs ( dFdy1, {x,y,Dy}, {(xim1+xi)/2,(yim1+yi)/2,(yi-yim1)/dx});
dFdy1N = subs ( dFdy1, {x,y,Dy}, {(xi+xip1)/2,(yi+yip1)/2,(yip1-yi)/dx});
EqF = simple((dFdyN+dFdyP)/2-(dFdy1N-dFdy1P)/dx)
dx =
1/5
EqF =
101*yi-99/2*yip1-99/2*yim1
Это уравнение зависит от xi-1, xi, xi+1, yi-1, yi, yi+1. Cформируем из него 3-диагональную систему уравнений. Коэффициенты при неизвестных этой системы – это коэффициенты при yi-1, yi, yi+1; правые части – это свободные члены. Заполним матрицу коэффициентов и вектор правых частей.
neq = nf-1 % количество уравнений
edx = eval(dx) % шаг сетки
xiC=[x1+edx:(x2-x1-2*edx)/neq:x2-edx]'; % текущая точка
xiP=xiC-edx;
xiN=xiC+edx; % предыдущая и последующая точки
e0 = subs(EqF,{xim1,xi,xip1,yim1,yi,yip1},{xiP,xiC,xiN,0,0,0} ); % своб. члены
e0 = ones(neq,1).*e0; % если скаляр, сделали вектором
eiP = subs ( EqF, {xim1,xi,xip1,yim1,yi,yip1}, {xiP,xiC,xiN,1,0,0} ) - e0;
eiC = subs ( EqF, {xim1,xi,xip1,yim1,yi,yip1}, {xiP,xiC,xiN,0,1,0} ) - e0;
eiN = subs ( EqF, {xim1,xi,xip1,yim1,yi,yip1}, {xiP,xiC,xiN,0,0,1} ) - e0;
b = -eval(e0); % правые части
A = diag(eval(eiC)) + diag(eval(eiN(1:neq-1)),1) + diag(eval(eiP(2:neq)),-1);
b(1) = b(1)-eiP(1)*y1; % учли граничные условия
b(neq) = b(neq)-eiN(1)*y2;
neq =
9
edx =
0.20000000000000
Решаем полученную систему и строим графики.
y = A\b; % решаем систему
x12a = linspace(x1,x2,nf+1); % абсциссы
y12a = zeros(nf+1,1);
y12a(2:nf) = y; % решение
y12a(1) = y1;
y12a(nf+1) = y2; % граничные условия
plot(xpl,y1a,'--b',x12a,y12a,'-r')
title ( '\bfExample 12a' ) % заголовок
xlabel('x')
ylabel('y(x)') % ось OY
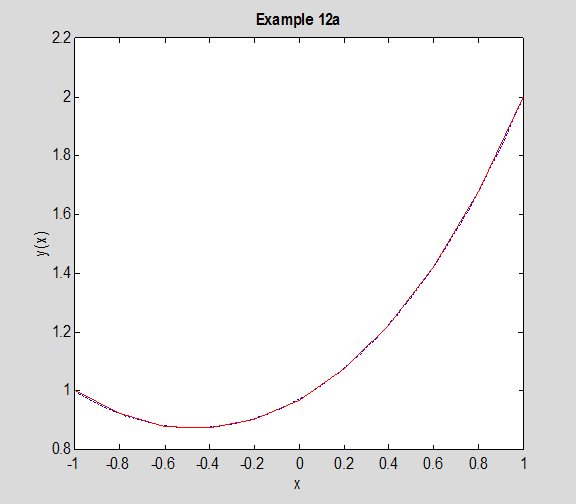
Рис. 12.1. Решение примера 12a
Ответ. Для 10 интервалов разбиения система уравнений МКР имеет вид
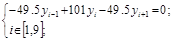 (12.7)
(12.7)
при этом в 1-е уравнение входит y0=1, а в 9-е уравнение y10=2. График экстремали показан на рис.12.1 сплошной красной линией, он практически сливается с теоретическим решением – штриховой синей линией.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|