Численные методы 2. Метод конечных разностей

12. Численные методы 2. Метод конечных разностей

12.1. Краткие теоретические сведения

В методе конечных разностей (МКР) экстремаль аппроксимируется кусочно-линейной функцией. Варьируются ординаты y(x) в заданных точках, и функционал становится функцией этих неизвестных ординат y₁, y₂, ….

Рассмотрим применение МКР к вариационной задаче для функционала (1.1, 1.2). Разобьём интервал [x₁,x₂] на n участков одинаковой длины Dx=(x₂-x₁)/n. Будем обозначать точки деления x_k. То есть граничные точки в этом примере в дальнейшем будем обозначать x₀ и x_n. Функционал J будет равен сумме функционалов на отдельных участках J_k. Так как участки малые, применим для вычисления интегралов формулу касательных: каждый из J_k равен подынтегральной функции, вычисленной в средней точке, и умноженной на ширину интервала:

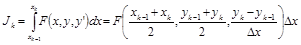. (12.1)

Функционал (1.1) будет функцией неизвестных ординат y₁, y₂, …, y_n_-1:

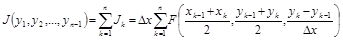. (12.2)

Значения y₀ и y_n известны – это заданные граничные условия. Для нахождения экстремума продифференцируем J по переменным y₁, y₂, …, y_n_-1, приравняем производные нулю и решим полученную систему уравнений. При вычислении ¶J/¶y_k учтём, что от y_k зависят только 2 слагаемых формулы (12.2): J_k и J_k₊₁.

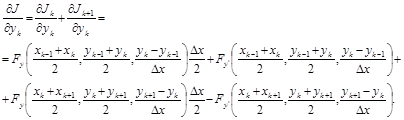(12.3)

После сокращения на Dx получим систему линейных алгебраических уравнений, которая своей структурой напоминает уравнение Эйлера (1.5):

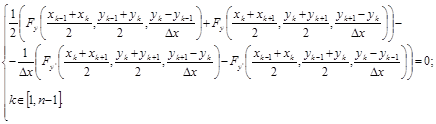(12.4)

Вместо F_y, которая фигурирует в уравнении Эйлера (1.5), в уравнении (12.4) – полусумма значений F_y на интервалах, примыкающих к точке x_k. Вместо dF_y_'/dx – отношение разности величин F_y_' справа и слева от точки x_k к ширине интервала Dx. Таким образом, (12.4) можно рассматривать как конечноразностный аналог уравнения Эйлера (1.5).

Аналогично выглядит конечноразностная аппроксимация уравнения Эйлера-Остроградского (4.6). Разобьём область D на n участков вдоль оси Ox: Dx=(x₂-x₁)/n и на m участков вдоль оси Oy: Dy=(y₂-y₁)/m. Будем обозначать узлы сетки x_i,y_k. Граничные точки в этом примере будут x₀, x_n, y₀, y_m. МКР-аппроксимация уравнения Эйлера-Остроградского (4.6) имеет вид

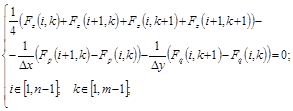(12.5)

где аргументы (i,k) для любой функции означают

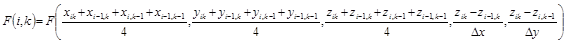. (12.6)

12 3 Следующая ⇒