II. Дифференциальные уравнения первого порядка.

II. Дифференциальные уравнения первого порядка.

Ранее определенное дифференциальное уравнение в общем виде можно записать так:

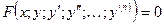
Например: ; ; .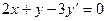

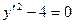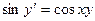Определение 1: Порядком дифференциального уравнения называется наибольший порядок производных, входящих в данное уравнение.

Например: 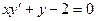- уравнение первого порядка;

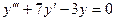- уравнение третьего порядка.

Определение 2: Дифференциальным уравнением первого порядка называется уравнение вида

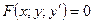(1)

Определение 3: Уравнение вида (2), полученное из уравнения (1), называется уравнением первого порядка, разрешенным относительно производной.

Иногда уравнения (1), (2) записывают в дифференциалах:

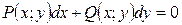Каждому дифференциальному уравнению соответствует, как правило, бесконечная совокупность его решений.

Определение 4: Всякое отдельно взятое решение дифференциального уравнения называется его частным решением.

Для многих дифференциальных уравнений первого порядка можно указать формулу вида 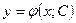или 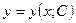(3), где 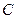- произвольная постоянная, такая, что при любом 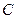функция (3) является решением уравнения (1) или (2), т.е. функция (3) представляет общее решение дифференциального уравнения (1) ил (2).

Определение 5: Выражение 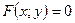или 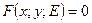(4) называют интегралом (частным, общим) дифференциального уравнения – оно является решением данного дифференциального уравнения в неявном виде.

Замечание: С геометрической точки зрения совокупность всех решений дифференциального уравнения представляет собой семейство кривых, называемых интегральными кривыми, а каждое частное решение представляет отдельную интегральную кривую.

⇐ Предыдущая 123 Следующая ⇒