
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задание№3. Задание №4.. Ресурсы. Изделия. Группа оборудования
Задание№3
- Найти уравнение прямой, проходящей через точку пересечения прямых
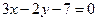 и
и  и отсекающей на оси абсцисс отрезок, равный 3.
и отсекающей на оси абсцисс отрезок, равный 3. - Найти проекцию точки А(-8, 12) на прямую, проходящую через точки В(2, -3) и С(-5, 1).
- Даны две вершины треугольника АВС: А(-4, 4), В(4, -12) и точка М(4,2) пересечения его высот. Найти вершину С.
- Найти уравнение прямой, отсекающей на оси ординат отрезок, равный 2, и проходящей параллельно прямой
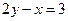 .
. - Найти уравнение прямой, проходящей через точку А(2, -3) и точку пересечения прямых
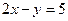 и
и  .
. - Доказать, что четырехугольник АВСД – трапеция, если А(3, 6), В(5, 2), С(-1, -3), Д(-5, 5).
- Записать уравнение прямой, проходящей через точку А(3, 1) перпендикулярно к прямой ВС, если В(2, 5), С(1, 0).
- Найти уравнение прямой, проходящей через точку А(-2, 1) параллельно прямой МN, если М(-3, -2), N(1, 6).
- Найти точку, симметричную точке М(2,-1) относительно прямой
 .
. - Найти точку О пересечения диагоналей четырехугольника АВСД, если А(-1, -3), В(3, 5), С(5, 2), Д(3, -5).
- Через точку пересечения прямых
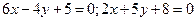 провести прямую, параллельную оси абсцисс.
провести прямую, параллельную оси абсцисс. - Известны уравнения стороны АВ треугольника АВС
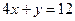 , его высот ВН:
, его высот ВН: 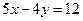 и АМ:
и АМ: 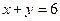 . Найти уравнения двух других сторон треугольника АВС.
. Найти уравнения двух других сторон треугольника АВС. - Даны две вершины треугольника АВС: А(-6, 2), В(2, -2) и точка пересечения его высот Н(1, 2). Найти координаты точки М пересечения стороны АС и высоты ВН.
- Найти уравнения высот треугольника АВС, проходящих через вершины А и В, если А(-4, 2), В(3, -5), С(5, 0).
- Вычислить координаты точки пересечения перпендикуляров, проведенных через середины сторон треугольника, вершинами которого служат точки А(2, 3), В(0, -3), С(6, -3).
- Составить уравнение высоты, проведенной через вершину А треугольника АВС, зная уравнения его сторон: АВ:
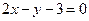 , АС:
, АС: 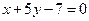 , ВС:
, ВС:  .
. - Дан треугольник с вершинами А(3, 1), В(-3, -1) и С(5, -12). Найти уравнение и вычислить длину его медианы, проведенной из вершины С.
- Составить уравнение прямой, проходящей через начало координат и точку пересечения прямых
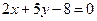 и
и 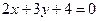 .
. - Найти уравнения перпендикуляров к прямой
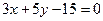 , проведенных через точки пересечения данной прямой с осями координат.
, проведенных через точки пересечения данной прямой с осями координат. - Даны уравнения сторон четырехугольника:
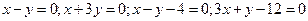 . Найти уравнения его диагоналей.
. Найти уравнения его диагоналей. - Составить уравнения медианы СМ и высоты СК треугольника АВС, если А(4, 6), В(-4, 0), С(-1, -4).
- Через точку Р(5, 2) провести прямую: а) отсекающую равные отрезки на осях координат; б)параллельную оси Ох; в) параллельную оси Оу.
- Записать уравнение прямой, проходящей через точку А(-2, 3) и составляющей с осью Ох угол:
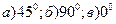 .
. - Какую ординату имеет точка С, лежащая на одной прямой с точками А(-6, -6) и В(-3, -1) и имеющая абсциссу, равную 3?
- Через точку пересечения прямых
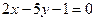 и
и 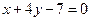 провести прямую, делящую отрезок между точками А(4, -3) и В(-1, 2) в отношении λ=2/3.
провести прямую, делящую отрезок между точками А(4, -3) и В(-1, 2) в отношении λ=2/3. - Известны уравнения двух сторон ромба
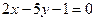 и
и 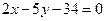 и уравнение одной из его диагоналей
и уравнение одной из его диагоналей  . Найти уравнение второй диагонали.
. Найти уравнение второй диагонали. - Найти точку Е пересечения медиан треугольника, вершинами которого являются точки А(-3, 1), В(7, 5) и С(5, -3).
- Записать уравнения прямых, проходящих через точку А(-1, 1) под углом
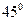 к прямой
к прямой 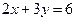 .
. - Даны уравнения высот треугольника АВС:
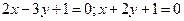 и координаты его вершины А(2, 3). Найти уравнения сторон АВ и АС треугольника.
и координаты его вершины А(2, 3). Найти уравнения сторон АВ и АС треугольника. - Даны уравнения двух сторон параллелограмма
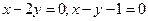 и точка пересечения его диагоналей М(3, -1). Найти уравнения двух других сторон.
и точка пересечения его диагоналей М(3, -1). Найти уравнения двух других сторон.
31. Составить уравнение плоскости, проходящей через точку М (-4; -3; -2) параллельно плоскости х + 2у – 3z – 6 = 0.
32.При каких значениях С и Д прямая 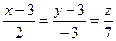 лежит в плоскости 2х–у+Сz+Д =0
лежит в плоскости 2х–у+Сz+Д =0
33.Составить уравнение прямой, проходящей через точку М (4; 7; -5) перпендикулярно двум прямым:
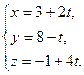 и
и 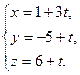
34. Написать уравнение перпендикуляра, опущенного из точки М (1; 1; 6) на прямую

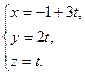
.35. Составить уравнение плоскости, проходящей через точку М (0; -3; 2) параллельно плоскости, проходящей через три точки М 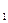 (0; -2; -1), М
(0; -2; -1), М 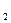 (1; -3; 4), М
(1; -3; 4), М 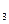 (1; 1; -1).
(1; 1; -1).
36. Найти расстояние от точки М (3; 5; 5) до прямой 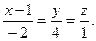
37. Найти расстояние от точки М (5; 4; -1) до плоскости, проходящей через точки М 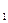 (0; 4; 0), М
(0; 4; 0), М 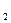 (0; 4; -3), М
(0; 4; -3), М 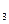 (3; 0; +3).
(3; 0; +3).
38. Прямая L проходит через точку М (3; -4; 0) и точку пересечения прямой 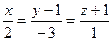 с плоскостью х+у-z+2=0. Найти величину угла, образованного прямой L с плоскостью 2х+у+2z-5=0.
с плоскостью х+у-z+2=0. Найти величину угла, образованного прямой L с плоскостью 2х+у+2z-5=0.
39. Написать уравнение плоскости, параллельной плоскости х-2у+2z-7+0=0 и отстоящей от точки М (4; 1; -3) на расстоянии d = 2.
40. Плоскость Lпроходит через точки М 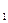 (-6; 1; -5), М
(-6; 1; -5), М 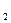 (7; -2; -1), М
(7; -2; -1), М 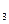 (10; -7; 1). Найти точку, симметричную точке (3; -4; -6) относительно плоскости L.
(10; -7; 1). Найти точку, симметричную точке (3; -4; -6) относительно плоскости L.
Задание №4.
1. Требуется изготовить не более 80 приборов типов А и В. Затраты на производство приборов типа А равны 2,7 ден. ед, типа В – 3 ден. ед. Общие затраты не должны превышать 200 ден. ед. прибыль, получаемая от продажи прибора типа А, равна 7,1 ден. ед., типа В – 8 ден. ед. Общая прибыль должна быть не менее 500 ден. ед. Построить на плоскости область допустимых планов производства приборов типа А и В.
2. Требуется перевезти не более 18 изделий I и не менее 23 изделий типа II. Изделия типа I перевозятся на корабле с затратами на единицу перевозимого изделия 4,3 ден. ед., а изделия типа II перевозятся на самолёте с затратами на единицу изделия 4,9 ден. ед. Суммарные затраты не должны превышать 180 ден. ед. Построить на плоскости область всевозможных вариантов перевозки изделий.
3. Требуется изготовить не более 250 изделий. Прибыль от реализации изделия типа А равна 5 ден. ед., типа В – 4,5 ден. ед. Затраты на производство товаров типов А и В равны 2,5 ден. ед., а общие затраты не должны превышать 450 ден. ед. Построить на плоскости область всевозможных объёмов производства изделий типов А и В, при условии, что прибыль будет не менее 690 ден. ед.
4. Цеха завода могут работать не более 23 дней в месяц. Затраты на электроэнергию в первом цеху составляют 15000 ден. ед в день, во втором – 18000 ден. ед. в день. Общие затраты на электроэнергию не должны превышать 700000 ден. ед. Первый цех приносит ежедневную прибыль в 40000 ден. ед., второй – 43000. Общая прибыль должна быть больше либо равной 1600000 ден. ед. Построить на плоскости область допустимых вариантов рабочих дней цехов в месяц.
5. Владелец фирмы по прокату автомобилей хочет закупить автомобили двух моделей А и В. Предположим, что автомобиль модели А стоит 300$, автомобиль модели В – 500$. Известно, что в гараже фирмы может поместиться не более 20 новых машин, а на закупку новых автомобилей ассигновано 7000$. Ожидаемая прибыль от эксплуатации одной машины модели А равна 100$, а от эксплуатации машины модели В – 140$. Построить на плоскости область допустимых вариантов покупки автомобилей А и В, если общая прибыль должна быть не меньше 1500$.
6. Требуется изготовить не менее 50 автомобилей типов "Джип" и "Кабриолет". Затраты на производство машины "Джип" равны 10000$, "Кабриолет" – 8500$. Общие затраты на производство автомобилей не должны превышать 65000$. Автомобили "Джип" и "Кабриолет" продают соответственно по 20000$ и 19000$. Общий доход от продаж должен быть не меньше 1000000$. Построить на плоскости  область допустимых планов выпуска автомобилей.
область допустимых планов выпуска автомобилей.
7. Цех выпускает трансформаторы видов А и Б. На один трансформатор вида А расходуется 5 кг трансформаторного железа и 3 кг трансформаторной проволоки, а на трансформатор Б - 3кг железа и 2кг проволоки. От реализации трансформатора вида А прибыль составляет 12 ден. ед., вида Б - 10 ден. ед.. Сменный фонд железа - 400 кг, проволоки - 300 кг. Записать в математической форме условия, которым должен удовлетворять план выпуска трансформаторов, если расход ресурсов не превышает выделенных фондов, а 156 прибыль не менее 900 ден. ед. за смену. Построить на плоскости  область допустимых планов выпуска трансформаторов.
область допустимых планов выпуска трансформаторов.
8. Цех производит изделия А и Б. Сменный плановый выпуск составляет 90 изделий А и 70 изделий Б. За смену не может использоваться более 540 ед. оборудования, более 550 ед. сырья и более 405 ед. электроэнергии. Расход ресурсов на одно изделие указан в таблице. От реализации изделия А прибыль составляет 80 ден. ед., изделия Б - 70 ден. ед.. Каким математическим условиям должен удовлетворять выпуск сверхплановой продукции, при котором выполняются ограничения на общий расход ресурсов и обеспечивается не менее 2800 ден. ед. прибыли?
Ресурсы
Изделия