
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Контрольная работа для студентов заочного отделения филиала УдГУ
Контрольная работа для студентов заочного отделения филиала УдГУ
ПОСЕЛОК Новый
Контрольная работа
Выбор варианта по списку
Задание №1
Проверить совместность системы уравнений и в случае совместности решить ее:
а) по формулам Крамера;
б) с помощью обратной матрицы (матричным методом);
в) методом Гаусса.
1. 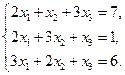 2.
2. 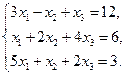 3.
3. 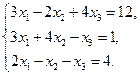
4. 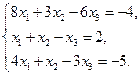 5.
5. 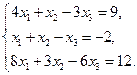 6.
6. 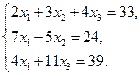
7. 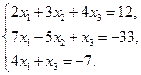 8.
8. 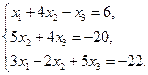 9.
9. 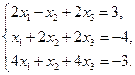
10. 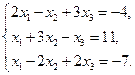 11.
11. 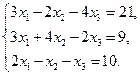 12.
12. 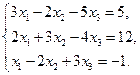
13. 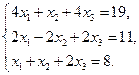 14.
14. 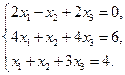 15.
15. 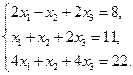
16. 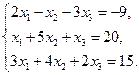 17.
17. 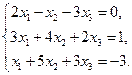 18.
18. 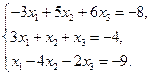
19. 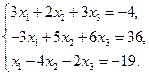 20.
20. 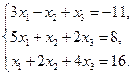 21.
21. 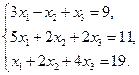
22. 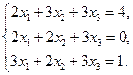 23.
23. 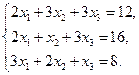 24.
24. 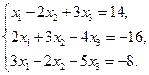
25. 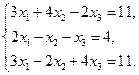 26.
26. 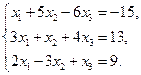 27.
27. 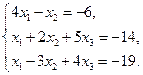
28. 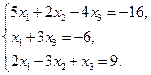 29.
29. 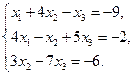 30.
30. 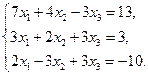
31. 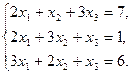 32.
32. 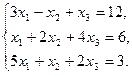 33.
33. 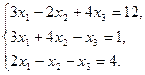
34. 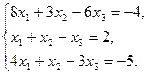 35.
35. 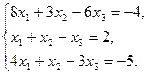 36.
36. 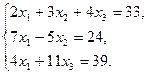
37. 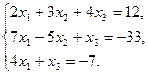 38.
38. 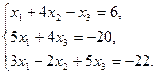 39.
39. 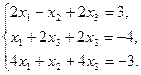
40. 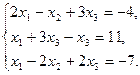
Задание №2
- Найти величины отрезков, отсекаемых на осях координат плоскостью, проходящей через точку М(-2, 7, 3) параллельно плоскости
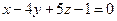 .
. - Составить уравнение плоскости, проходящей через середину отрезка
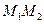 перпендикулярно к этому отрезку, если
перпендикулярно к этому отрезку, если 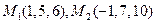 .
. - Найти расстояние от точки М(2; 0; -0,5) до плоскости
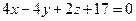 .
. - Составить уравнение плоскости, проходящей через точку А(2, -3, 5) параллельно плоскости Оху.
- Составить уравнение плоскости, проходящей через ось Ох и точку А(2, 5, -1).
- Составить уравнение плоскости, проходящей через точки А(2, 5, -1), В(-3, 1, 3) параллельно оси Оу.
- Составить уравнение плоскости, проходящей через точку А(3, 4, 0) и прямую
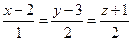 .
. - Составить уравнение плоскости, проходящей через две параллельные прямые
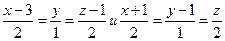 .
. - Составить уравнение плоскости в отрезках, если она проходит через точку М(6, -10, 1) и отсекает на оси Ох отрезок а=-3, а на оси Оz – отрезок с=2.
- Составить уравнение плоскости, проходящей через точку А(2, 3, -4) параллельно двум векторам
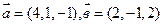 .
. - Составить уравнение плоскости , проходящей через точки А(1, 1, 0), В( 2, -1, -1) перпендикулярно к плоскости
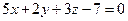 .
. - Составить уравнение плоскости, проходящей через начало координат перпендикулярно к двум плоскостям
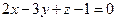 и
и 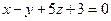 .
. - Составить уравнение плоскости, проходящей через точки А(3, -1, 2), В(2, 1, 4) параллельно вектору
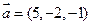 .
. - Составить уравнение плоскости, проходящей через начало координат перпендикулярно к вектору
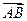 , если А(5, -2, 3), В(1, -3, 5).
, если А(5, -2, 3), В(1, -3, 5). - Найти величины отрезков, отсекаемых на осях координат плоскостью, проходящей через точку М(2, -3, 3) параллельно плоскости
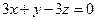 .
. - Составить уравнение плоскости, проходящей через точку М(1, -1, 2) перпендикулярно к вектору
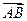 , если А(2, 3, -4), В(-1, 2, -3).
, если А(2, 3, -4), В(-1, 2, -3). - Показать, что прямая
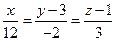 параллельна плоскости
параллельна плоскости 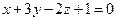 , а прямая
, а прямая 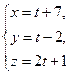 лежит в этой плоскости.
лежит в этой плоскости. - Составить общее уравнение плоскости, проходящей через точку А(3, -4, 1) параллельно координатной плоскости Охz.
- Составить уравнение плоскости, проходящей через ось Оу и точку М(3, -5, 2).
- Составить уравнение плоскости, проходящей через точки М(1, 2, 3) и N(-3, 4, -5) параллельно оси Оz.
- Составить уравнение плоскости, проходящей через точку М(2, 3, -1) и прямую
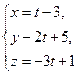
- Найти проекцию точки М(4, -3, 1) на плоскость
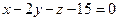 .
. - Определить, при каком значении В плоскости
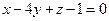 и
и 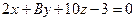 будут перпендикулярны.
будут перпендикулярны. - Составить уравнение плоскости, которая проходит через точку М(2, -3, -4) и отсекает на осях координат отличные от нуля отрезки одинаковой величины.
- При каких значениях n и А прямая
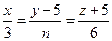 перпендикулярна к плоскости
перпендикулярна к плоскости 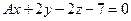 ?
? - Составить уравнение плоскости, проходящей через точки А(2, 3, -1), В(1, 1, 4) перпендикулярно к плоскости
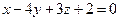 .
. - Составить уравнение плоскости, проходящей через начало координат перпендикулярно к плоскостям
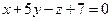 и
и 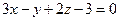 .
. - Составить уравнение плоскости, проходящей через точки М(2, 3, -5) и N(-1, 1, -6) параллельно вектору
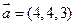 .
. - Определить, при каком значении С плоскости
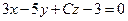 и
и 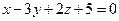 будут перпендикулярны.
будут перпендикулярны.
30. Через точку пересечения прямых 3x + 2y – 4 = 0 и x – 5y + 8 = 0 проведены прямые, одна из которых проходит через начало координат, а другая параллельна оси Ox. Составить их уравнения.
 31. Составить каноническое уравнение прямой, лежащей в плоскости Оху, проходящей через начало координат и перпендикулярно к прямой
31. Составить каноническое уравнение прямой, лежащей в плоскости Оху, проходящей через начало координат и перпендикулярно к прямой 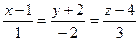
32.Найти координаты точки, симметричной точке 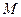 (2; 8; 0) относительно прямой
(2; 8; 0) относительно прямой
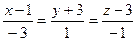 .
.
33. Найти расстояние между параллельными плоскостями: х+у–z–2 =0 и 2х+2у-2z+5=0
34. Составить уравнение плоскости, проходящей через точку M (4; -3; 6) перпендикулярно прямой 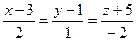
35. Составить уравнение прямой, проходящей через точку M (1; -2; 3) и перпендикулярной с прямым 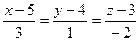 ,
, 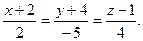
36. Найти координаты проекции точки М (-3; 0; 2) на прямую 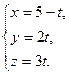
37. Найти расстояние между параллельными плоскостями: 2х – 3у + 6z – 14 = 0 и
2х – 3у + 6z + 42 = 0.
38. Найти координаты проекции точки 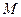 (2; 2; -2) на плоскость 3х – у + z – 13 = 0
(2; 2; -2) на плоскость 3х – у + z – 13 = 0
39. Составить уравнение прямой, проходящей через точку М (2; -3; 5) перпендикулярно двум прямым: 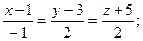
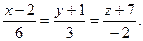
40. Найти координаты точки пересечения прямой 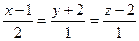 с плоскостью 3х – у + 2z + 5 = 0.
с плоскостью 3х – у + 2z + 5 = 0.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|