Элементы пирамиды ABCDE. Правильная пирамида SABCD. Прямоугольная пирамида FABCD

Элементы пирамиды ABCDE

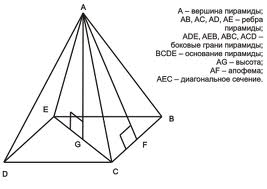
апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины А;

боковые грани — треугольники, сходящиеся в вершине пирамиды;

боковые ребра — общие стороны боковых граней;

вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания;

высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра) (Н);

диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания;

основание — многоугольник, которому не принадлежит вершина пирамиды.

Правильная пирамида SABCD

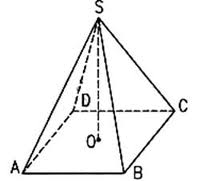Пирамида называется правильной, если основанием её является правильный многоугольник, а вершина проецируется в центр основания. Тогда она обладает такими свойствами: боковые ребра правильной пирамиды равны; в правильной пирамиде все боковые грани — равные равнобедренные треугольники; в любую правильную пирамиду можно как вписать, так и описать около неё сферу;

Прямоугольная пирамида FABCD

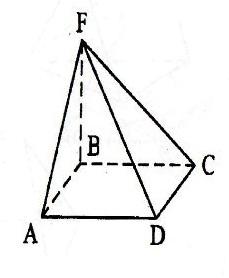
Пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию. В данном случае, это ребро и является высотой пирамиды.

Усечённая пирамида

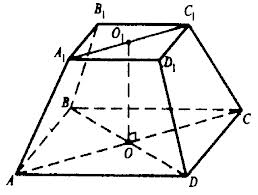
Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.

Боковая поверхность — это сумма площадей боковых граней.

Для нахождения боковой поверхности в правильной пирамиде можно использовать формулу:

S_б.п.= 1/2•Р•ℓ

Полная поверхность — это сумма площади боковой поверхности и площади основания.

Для нахождения полной поверхности в правильной пирамиде можно использовать формулу:

S_п.п. = 1/2•Р•ℓ+S_осн.

Объем пирамиды (любой) может быть вычислен по формуле: V = 1/3•S_осн.•Н

Решение задач:

⇐ Предыдущая 123 Следующая ⇒