
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ПЛОСКОПАРАЛЛЕЛЬНОЕ. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА. ПЛОСКОПАРАЛЛЕЛЬНОЕ. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
ПЛОСКОПАРАЛЛЕЛЬНОЕ
ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
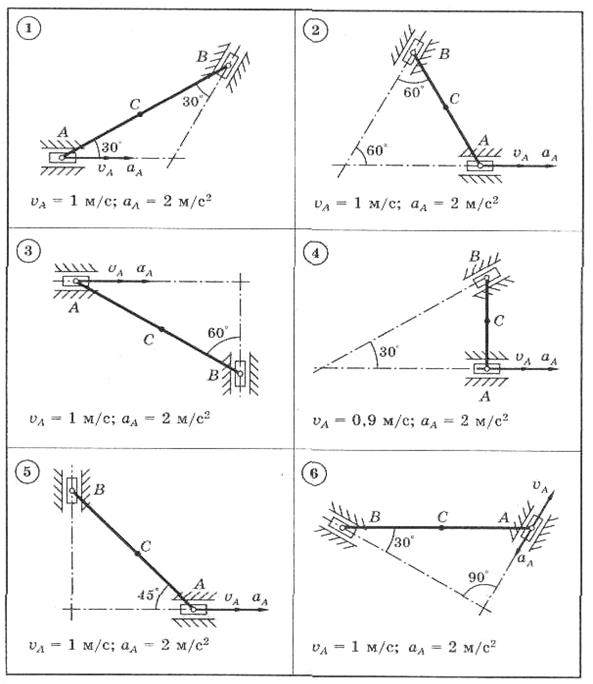
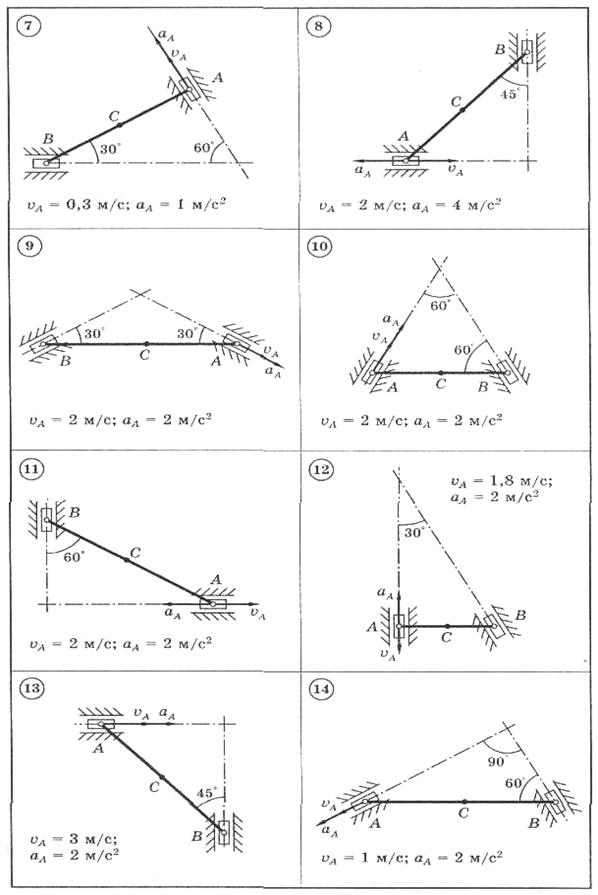
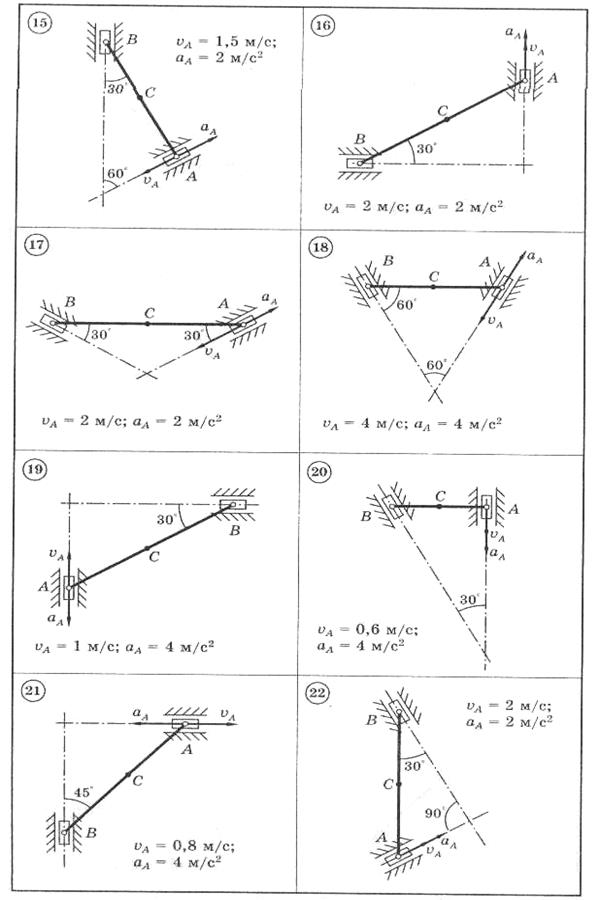
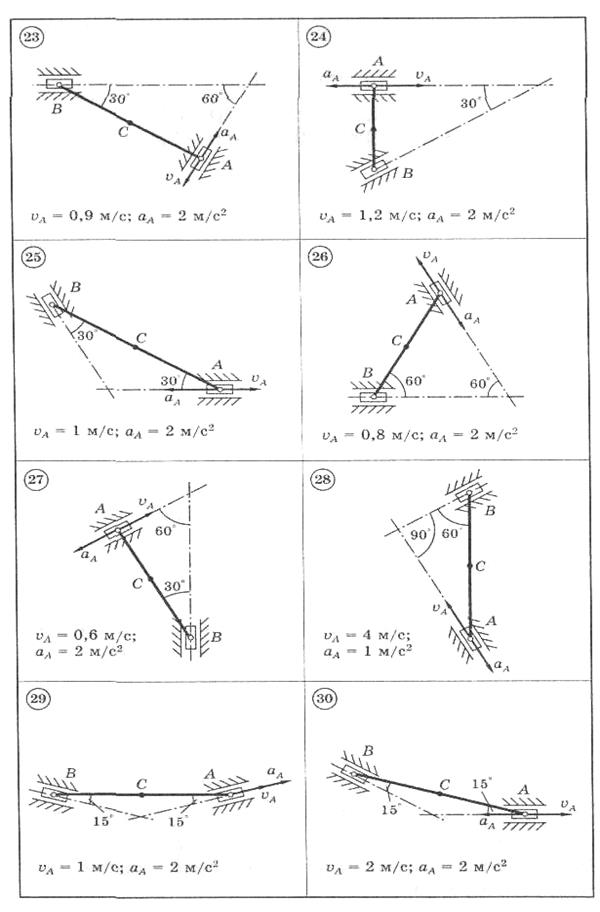
Для представленных на схемах 1-30 механизмов, состоящих из шатуна АВ длиной 2 м и двух ползунов, по заданным величинам скорости и ускорения ползуна А определить скорость и ускорение ползуна В и средней точки С шатуна, а также угловую скорость и угловое ускорение шатуна.
 |
 |
 |
 |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ПЛОСКОПАРАЛЛЕЛЬНОЕ
ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
ЗАДАЧА 1
Колесо радиуса r = 1 м катится без скольжения ускоренно по прямолинейному рельсу, имея в данный момент времени скорость центра
vo = 1 м/с и ускорение центра 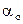 = 1 м/с2 (рис.3). Определить угловую скорость и угловое ускорение колеса, скорости и ускорения точек его обода
= 1 м/с2 (рис.3). Определить угловую скорость и угловое ускорение колеса, скорости и ускорения точек его обода
М1, М2, М3, и М4, а также установить положение МЦС и МЦУ колеса.
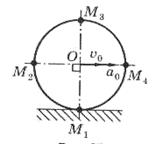 | 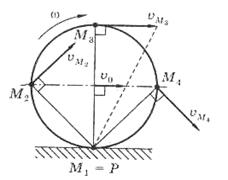 | ||
Рис. 3 Рис. 4
Решение.
1. Определение скоростей. У колеса, катящегося без скольжения по неподвижной поверхности, МЦС (точка Р) находится в точке касания с этой поверхностью (рис 4). В данном случае это точка М1 (М1 = Р): v 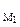 = 0.
= 0.
Скорости точек плоской фигуры пропорциональны расстояниям от этих точек до МЦС: v 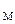 = ω│МР│, где ω - угловая скорость тела. Применяем эту формулу к точке О: vо = ω│ОР│ = ωr , откуда ω = vo/r = 1 c-1.
= ω│МР│, где ω - угловая скорость тела. Применяем эту формулу к точке О: vо = ω│ОР│ = ωr , откуда ω = vo/r = 1 c-1.
Для точек М2 и М3 расстояния до точки Р одинаковы, поэтому одинаковы и модули скоростей этих точек:
v 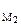 = v
= v 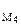 = ω│M2P│ = ωr
= ω│M2P│ = ωr 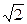 = vo
= vo 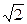 =
= 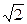 м/с.
м/с.
Скорость точки М3 v 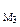 = ω│M3P│ = ω2r = 2vo = 2 м/с.
= ω│M3P│ = ω2r = 2vo = 2 м/с.
Направления скоростей перпендикулярны отрезкам, соединяющим точки с МЦС.
Для вычисления скоростей можно было использовать также и теорему о сложении скоростей, выбрав в качестве полюса центр колеса: 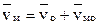 , где vмо = ω│МО│. Скорость
, где vмо = ω│МО│. Скорость 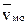 перпендикулярна отрезку МО и направлена по ходу вращения.
перпендикулярна отрезку МО и направлена по ходу вращения.
Можно было также пользоваться и следствием из этой теоремы о равенстве проекций скоростей точек на ось, проходящую через эти точки.
2. Определение ускорений. Вычислим сначала угловое ускорение колеса, формально дифференцируя выражение угловой скорости
ε = 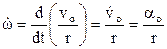 = 1 с-2
= 1 с-2
В данном случае использован тот факт, что движение центра колеса прямолинейное и, следовательно, касательное ускорение точки 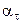 =
= 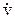 совпадает с полным ускорением.
совпадает с полным ускорением.
Для вычисления ускорений точек колеса применим теорему о сложении ускорений: 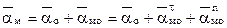 , выбрав в качестве полюса центр колеса. Вращательное ускорение точки относительно полюса
, выбрав в качестве полюса центр колеса. Вращательное ускорение точки относительно полюса 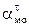 = ε│МО│ и направлено перпендикулярно отрезку МО по ходу углового ускорения, а центростремительное
= ε│МО│ и направлено перпендикулярно отрезку МО по ходу углового ускорения, а центростремительное 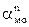 =ω2│МО│ всегда направлено от точки к полюсу.
=ω2│МО│ всегда направлено от точки к полюсу.
Тогда для точек М1, М2, М3, и М4 получим 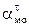 = εr = 1 м/с2,
= εr = 1 м/с2,
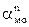 = ω2r = 1 м/с2. Направления их показаны на рис. 5.
= ω2r = 1 м/с2. Направления их показаны на рис. 5.
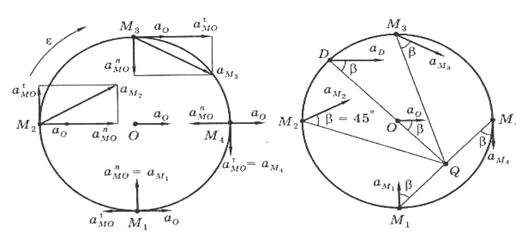 |
Рис. 5 Рис. 6
Складывая в каждой точке три вектора, модули которых равны по
1 м/с2, получаем 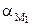 =
= 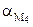 = 1 м/с2,
= 1 м/с2, 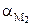 =
= 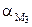 =
=  м/с2.
м/с2.
3. Определение положения МЦУ. Найти положение МЦУ (точки Q, ускорение которой равно нулю) можно на основании известных положений:
а) все ускорения составляют один и тот же угол 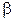 с направлениями из этих точек на МЦУ:
с направлениями из этих точек на МЦУ:
tg 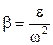 .
.
В данном случае tg 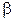 = 1 и
= 1 и 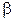 = 45о. Повернув каждое ускорение на угол
= 45о. Повернув каждое ускорение на угол 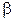 по ходу углового ускорения, мы на пересечении лучей и получим точку Q (рис. 6). Итак, МЦУ колеса при принятых исходных данных оказывается на середине отрезка М1М4;
по ходу углового ускорения, мы на пересечении лучей и получим точку Q (рис. 6). Итак, МЦУ колеса при принятых исходных данных оказывается на середине отрезка М1М4;
б) ускорения точек пропорциональны расстояниям от этих точек до МЦУ:
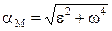 │МQ│.
│МQ│.
В силу одинаковости расстояний до МЦУ в данном случае оказываются равны между собой модули ускорений 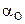 =
= 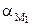 =
= 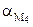 , а также
, а также 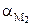 =
= 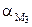 . Из всех точек колеса самое большое ускорение будет иметь точка D (рис. 6 )
. Из всех точек колеса самое большое ускорение будет иметь точка D (рис. 6 )
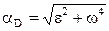 │DQ│=
│DQ│= 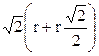 = 1 +
= 1 + 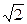 м/с2.
м/с2.
О т в е т:
ω = 1 с-1; ε = 1 с-2; v 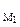 = 0; v
= 0; v 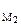 = v
= v 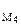 =
= 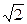 м/с;
м/с;
v 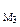 = 2 м/с;
= 2 м/с; 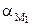 =
= 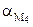 = 1 м/с2;
= 1 м/с2; 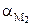 =
= 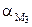 =
=  м/с2.
м/с2.
 ЗАДАЧА 2
ЗАДАЧА 2
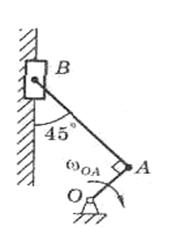
Кривошип ОА длиной 0,2 м вращается
равномерно с угловой скоростью ωОА = 10 с-1 и
приводит в движение шатун АВ длиной 1 м. Ползун
В движется по вертикали. Найти угловую скорость
и угловое ускорение шатуна, а также скорость и
ускорение ползуна в момент, когда кривошип и
шатун взаимно перпендикулярны и образуют с
вертикалью угол 45о (рис. 7).
Рис. 7
Решение.
1. Определение скоростей. Вычислим скорость точки А как точки вращающегося кривошипа:
vА = ωОА│ОА│ = 2 м/с.
Она направлена перпендикулярно ОА (рис. 8).
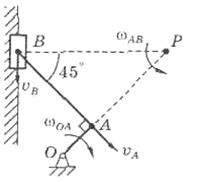 Скорость vВ ползуна направлена по
Скорость vВ ползуна направлена по
направляющей вертикально.
Для шатуна АВ, совершающего
плоское движение, теперь известны
направления скоростей двух его точек:
А и В. Восставляя перпендикуляры
к векторам этих скоростей, находим
точку Р их пересечения – МЦС шатуна.
Используя известную формулу
для скоростей точек при плоском Рис. 8
 движении, получаем
движении, получаем
vА = ωАВ│АР│; vВ = ωАВ│ВР│.
Из треугольника АВР имеем
│АР│ = 1 м; │ВР│ = 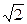 м, и тогда
м, и тогда
ωАВ = 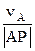 = 2 с-1; vВ = 2
= 2 с-1; vВ = 2 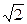 м/с.
м/с.
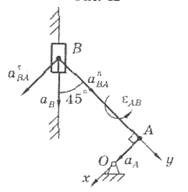
2. Определение ускорений.
Вычислим сначала ускорение
точки А как точки кривошипа:
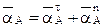 . Рис. 9
. Рис. 9
Здесь вращательное ускорение
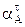 = εОА│ОА│ = 0, так как εОА =
= εОА│ОА│ = 0, так как εОА = 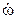 ОА = 0, поскольку ωОА = const.
ОА = 0, поскольку ωОА = const.
Тогда полное ускорение точки А равно центростремительному
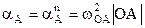 = 20 м/с2
= 20 м/с2
и направлено к оси вращения – точке О (рис. 9).
Для вычисления ускорения точки В воспользуемся теоремой о сложении ускорений, взяв точку А в качестве полюса:
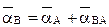 =
= 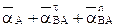 . (*)
. (*)
Центростремительное ускорение точки В в относительном вращениивокруг точки А по модулю равно
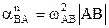 = 4 м/с2, и направлено от точки В к полюсу – точке А.
= 4 м/с2, и направлено от точки В к полюсу – точке А.
Модуль вращательного ускорения 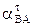 определяется по формуле
определяется по формуле
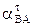 = εАВ│АВ│ и пока не может быть вычислен, поскольку неизвестна величина углового ускорения εАВ . Направление вектора
= εАВ│АВ│ и пока не может быть вычислен, поскольку неизвестна величина углового ускорения εАВ . Направление вектора 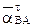 также не может быть определено однозначно, так как неизвестно направление углового ускорения, т.е. неизвестно, ускоренным или замедленным является поворот шатуна. Примем пока этот поворот ускоренным, тогда направление
также не может быть определено однозначно, так как неизвестно направление углового ускорения, т.е. неизвестно, ускоренным или замедленным является поворот шатуна. Примем пока этот поворот ускоренным, тогда направление 
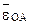

совпадает с направлением 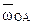 , а вектор
, а вектор 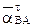 направим перпендикулярно отрезку ВА по ходу углового ускорения.
направим перпендикулярно отрезку ВА по ходу углового ускорения.
Вектор ускорения точки В направлен по вертикальной прямолинейной направляющей. Будем пока считать движение ползуна ускоренным и направим ускорение 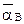 в ту же сторону, что и скорость
в ту же сторону, что и скорость 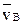 (рис. 8, 9).
(рис. 8, 9).
Теперь в равенстве (*) все ускорения имеют определенное направление, и мы можем записать это уравнение в проекциях на выбранные оси:
х: 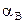 sin45o =
sin45o = 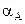 +
+ 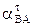 ; y:
; y: 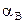 cos45o =
cos45o = 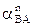 .
.
Из последнего уравнения получаем 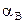 =
= 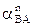
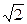 = 4
= 4 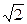 м/с2, тогда из первого уравнения
м/с2, тогда из первого уравнения 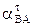 =
= 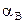
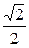 -
- 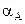 = -16 м/с2.
= -16 м/с2.
Отсюда следует, что
εАВ = 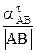 = -16 с-2.
= -16 с-2.
Отрицательные знаки у величин 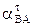 и εАВ показывают, что их истинные направления противоположны принятым.
и εАВ показывают, что их истинные направления противоположны принятым.
О т в е т: ωАВ = 2 с-1; εАВ = -16 с-2; vВ = 2 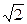 м/с;
м/с; 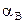 = 4
= 4 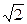 м/с2.
м/с2.
ЗАДАНИЕ К3
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|