ПРОСТЕЙШИЕ ВИДЫ. ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА

ПРОСТЕЙШИЕ ВИДЫ

ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА

ЗАДАЧА 1

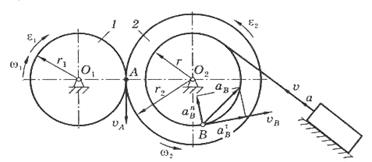Лебедка (рис. 1), поднимающая груз по наклонной плоскости, состоит из двух валов 1 и 2 с шестернями (зубчатыми колесами), числа зубьев которых равны соответственно z₁ =12 и z₂=48. К валу 2 прикреплен барабан радиусом r = 0,3 м, на который наматывается грузовой трос. Вал 1 вращается равноускоренно с угловым ускорением ε₁ = 8 с^-2. Определить скорость, ускорение и перемещение груза, а также ускорение точки В барабана в момент времени t = 1 с. В начальный момент времени система находилась в покое.

Рис. 1.

Решение.Найдем угловую скорость ω₁ ведущего вала 1 из условия, что он вращается с угловым ускорением ε₁ = const, учитывая, что 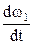= ε₁. Интегрируя последнее уравнение по времени, получаем ω₁= 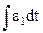=ε₁ + C₁.

Постоянную интегрирования получаем из начального условия: при t = 0 ω₁= 0 (система находилась в покое), следовательно, C₁ =0.

Итак, угловая скорость вала 1 определяется уравнением ω₁ = ε₁t = 8t.

При t = 1 с получаем ω₁ = 8 с^-1.

Шестерни 1 и 2 взаимодействуют без проскальзывания. Поэтому скорости точек их касания (точка А) будут одинаковы: ω₁r₁= ω₂r₂.

Отсюда находим угловую скорость ω₂ вала 2, учитывая, что :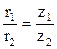

ω₂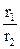=ω₁= ω₁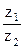= 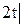_t₌₁_c = 2 c^-1.

Угловое ускорение вала 2 равно ε₂ = 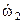= 2 с^-2.

Поскольку трос нерастяжим и относительно барабана не проскальзывает, то скорость груза v будет равна скорости любой из точек на ободе барабана, в частности, скорости точки В: v = v _В = ω₂r = 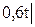_t₌₁_c = 0,6 м/с.

Ускорение точки В равно векторной сумме касательного (вращательного) и нормального (центростремительного) ускорений:

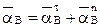Направление вращательного ускорения определяется направлением углового ускорения ε₂, а его модуль равен 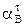= ε₂r = 0,6 м/с². Центростремительное ускорение направлено к оси вращения вала 2 и равно по модулю 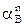= 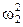r = 1,2 м/с².

Модуль ускорения точки В

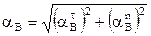            = 1,34 м/с².

Ускорение груза можно найти, взяв производную по времени от его скорости, так как это касательное ускорение: 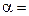= 0,6 м/с² .

Перемещение груза определяется интегрированием модуля скорости по времени:

          s = 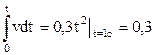м.

Ответ: v =0,6 м/с; а = 0,6 м/с²; s = 0,3 м; а_В = 1,34 м/с².



                                                     ЗАДАЧА 2

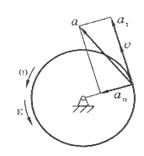
Маховик радиусом R = 0,5 м вращается так, что его угловая скорость меняется в соответствии с уравнением ω = 0,25е²^tc^-1. Для момента времени   t = 0,5 с после начала движения определить скорость и ускорение точки на ободе маховика. Установить, за какое время маховик сделает 100 полных оборотов.

Решение. Для момента времени t = 0,5 с получаем ω = 0,680 с^-1, и скорость точки на ободе маховика равна v = ωR = 0,340 м/с.

Угловое ускорение маховика

ε = 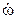= 0,5е²^t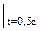= 1,36 c^-2.

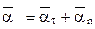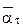Ускорение точки на ободе маховика равно сумме двух составляющих ускорений: , где   и 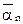- касательное (вращательное) и нормальное (центростремительное) ускорения точки.

Учитывая, что вращательное ускорение равно по модулю 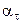= εR, найдем 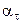= 0,680 м/с²; центростремительное ускорение 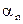= ω²R = 0,231 м/с².

Модуль полного ускорения точки

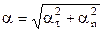= 0,718 м/с.

Направления скорости и ускорений показаны

на рис. 2.

Поскольку    значения     величин      угловой

скорости и углового ускорения имеют одинаковые

знаки,   вращение тела ускоренное. Соответственно,

совпадают по направлению угловая скорость и

угловое ускорение тела, а также скорость точки и                      Рис. 2

вращательное ускорение.

Поворот маховика на 100 полных оборотов соответствует углу его поворота φ =200π рад. Выражение для угла поворота найдем из уравнения

ω = 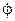. Имеем

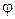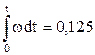= е²^t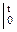= 0,125(е²^t – 1).

Итак, 0,125(е²^t – 1) = 200π, откуда находим t = 4,26 с.

Ответ: v = 0,340 м/с; 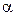= 0,718 м/с²;   t = 4,26 с.



ЗАДАНИЕ К2

⇐ Предыдущая 1 234 5 Следующая ⇒