Объём параллелепипеда

Объём параллелепипеда

Теорема. Объём прямоугольного параллелепипедa равен произведению трёх его измерений:V=abc.

Доказательство:

1. Прямоугольный параллелепипед с измерениями a=1 b=1 c=1 имеет объем V=1 – выполняется

2. Рассмотрим два прямоугольных параллелепипеда с измерениями a,b,c и a¢, b¢, c¢, такие, что a=a¢, b=b¢, c=c¢. Тогда V₁=abc, V₂=a¢b¢c¢, откуда получаем, что V₁= V₂

3. Рассмотрим многогранник, представляющий собой сумму параллелепипедов Р и P¢:

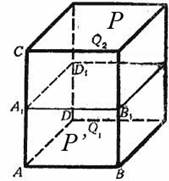
Тогда будем иметь: V = АВ•АС•АD, V_P_¢ = АВ• АА₁•АD, V_P= А₁В₁•А₁С•А₁D₁. Складывая почленно два последних равенства и замечая, что А₁В₁ = АВ и А₁D₁=АD, получим: V_P_¢+ V_P= АВ• АА₁•АD+АВ•А₁С•АD = АВ•АD (АА₁ + А₁С) =АВ•АD•АC, отсюда получаем: V_P_¢+ V_P = V■

Замечание: Так как произведение аb выражает площадь основания, то можно сказать, что объём прямоугольного параллелепипеда равен произведению площади основания на высоту.

Теорема: Наклонная призма равновелика такой прямой призме, основание которой равно ортогональному сечению наклонной призмы, а высота — её боковому ребру.

Доказательство: Пусть дана наклонная призма ABCDEA₁B₁C₁D₁E₁

Продолжим все её боковые рёбра и боковые грани в одном направлении.

Возьмём на продолжении одного какого-нибудь ребра произвольную точку а и проведём через неё перпендикулярное Затем, отложив аа₁ = АА₁, проведём через а₁ перпендикулярное сечение a₁b₁c₁d₁e₁. Так как плоскости обоих сечений параллельны, то bb₁ = сс₁ = dd₁ = ее₁ = аа₁ = АА₁ сечение abcde.

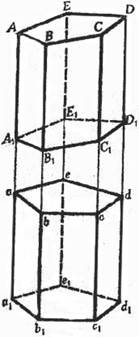
Вследствие этого многогранник a₁d, у которого за основания приняты проведённые нами сечения, есть прямая призма, о которой говорится в теореме. Докажем, что данная наклонная призма равновелика этой прямой. Для этого предварительно убедимся, что многогранники aD и a₁D₁ равны. Основания их abcde и a₁b₁c₁d₁e₁ равны как основания призмы a₁d; с другой стороны, прибавив к обеим частям равенства А₁А = а₁а по одному и тому же отрезку прямой А₁а, получим: аА = а₁А₁; подобно этому bВ = b₁В₁, сС = с₁С₁ и т. д. Вообразим теперь, что многогранник aD вложен в многогранник a₁D₁ так, что основания их совпали; тогда боковые рёбра, будучи перпендикулярны к основаниям и соответственно равны, также совпадут; поэтому многогранник aD совместится с многогранником a₁D₁; значит, эти тела равны. Теперь заметим, что если к прямой призме a₁d добавим многогранник aD, а к наклонной призме A₁D добавим многогранник a₁D₁, равный aD, то получим один и тот же многогранник a₁D. Из этого следует, что две призмы A₁D и a₁d равновелики.

Теорема. Объём параллелепипеда равен произведению площади основания на высоту.

Доказательство: Ранее мы доказали эту теорему для параллелепипеда п р я м о у г о л ь н о г о, теперь докажем её для параллелепипеда п р я м о г о, а потом и н а к л о н н о г о.

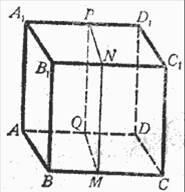
1). Пусть А…С₁ — прямой параллелепипед, т. е. такой, у которого основание ABCD — какой-нибудь параллелограмм, а все боковые грани — прямоугольники. Возьмём в нём за основание боковую грань АА1В1В; тогда параллелепипед будет н а к л о н н ы й. Рассматривая его как частный случай наклонной п р и з м ы, на основании предыдущей теоремы можно утверждать, что этот параллелепипед равновелик такому прямому параллелепипеду, у которого основание есть перпендикулярное сечение MNPQ, а высота ВС.

Четырёхугольник MNPQ— прямоугольник, потому что его углы служат линейными углами прямых двугранных углов; поэтому прямой параллелепипед, имеющий основанием прямоугольник MNPQ, должен быть прямоугольным и, следовательно, его объём равен произведению трёх его измерений, за которые можно принять отрезки МN, МQ и ВС. Таким образом,

V_A…С1 = МN • МQ • ВС = МN•(МQ•ВС).

Но произведение МQ•ВС выражает площадь параллелограмма АВСD, поэтому

V_A…С1 = S_АВСD•МN = S_АВСD • ВВ₁.

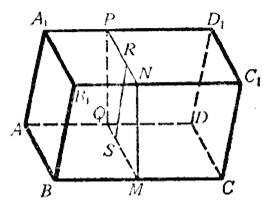
2) Пусть А…С1 — наклонный параллелепипед. Он равновелик такому прямому, у которого основанием служит перпендикулярное сечение МNРQ (т. е. перпендикулярное к рёбрам АD, ВС, . . .), а высотой — ребро ВС. Но, по доказанному, объём прямого параллелепипеда равен произведению площади основания на высоту; значит, V_А…С1 = S_МNРQ• ВС Если RS есть высота сечения МNРQ, то площадь S_МNРQ = МQ• RS, поэтому

V_А…С1 = МQ• RS • ВС = (ВС • MQ) • RS.

Произведение ВС • MQ выражает площадь параллелограмма АВСD; следовательно, объём V_А…С1 = S _АВСD• RS.

Остаётся теперь доказать, что отрезок RS представляет собой высоту параллелепипеда. Действительно, сечение МNРQ, будучи перпендикулярно к рёбрам ВС, В₁С₁, .. . , должно быть перпендикулярно к граням АВСD, ВВ₁С₁С, .... проходящим через эти рёбра. Поэтому если мы из точки S восставим перпендикуляр к плоскости АВСD, то он должен лежать весь в плоскости МNРQ и, следовательно, должен слиться с прямой RS, лежащей в этой плоскости и перпендикулярной к МQ. Значит, отрезок SR есть высота параллелепипеда. Таким образом, объем и наклонного параллелепипеда равен произведению площади основания на высоту.■

⇐ Предыдущая 1 23