Пирамида. Объем призмы и пирамиды

Пирамида

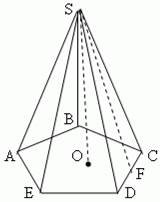
Пирамида – это многогранник, у которого одна грань (основание пирамиды) – это произвольный многоугольник (ABCDE), а остальные грани (боковые грани) – треугольники с общей вершиной S, называемой вершиной пирамиды. Перпендикуляр SO, опущенный из вершины пирамиды на её основание, называется высотой пирамиды. В зависимости от формы многоугольника, лежащего в основании, пирамида может быть соответственно: треугольной, четырёхугольной, пятиугольной, шестиугольной и т.д. Треугольная пирамида является тетраэдром (четырёхгранником), четырёхугольная – пятигранником и т.д.

Пирамида называется правильной, если в основании лежит правильный многоугольник, а её высота падает в центр основания. Все боковые рёбра правильной пирамиды равны; все боковые грани – равнобедренные треугольники. Высота боковой грани (SF) называется апофемой правильной пирамиды.

Теорема: Боковая поверхность правильной пирамиды равна половине произведения периметра основания на апофему

Доказательство самостоятельно

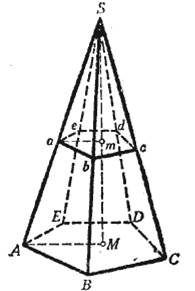
Теорема. Если пирамида пересечена плоскостью, параллельной основанию, то: 1) боковые рёбра и высота делятся этой плоскостью на пропорциональные части; 2) в сечении получается многоугольник (abcde), подобный основанию; 3) площади сечения и основания относятся, как квадраты их расстояний от вершины. Доказательство: 1) Прямые ab и АВ можно рассматривать как линии пересечения двух параллельных плоскостей (основания и секущей) третьей плоскостью ASB; поэтому ab||AB. По этой же причине bc||BC, cd||CD, ... и ат||АM; вследствие этого Sa/aA= Sb/bB = Sc/cC = ... = Sm/mM

2) Из подобия треугольников ASB и aSb, затем BSC и bSc и т. д. выводим:

AB/ab = BS/bs ; BS/bs = BC/bc ,

откуда

AB/ab = BC/bc

Так же

BC/bc = CS/cs ; CS/cs = CD/cd откуда BC/bc= CD/cd .

Аналогично доказывается пропорциональность остальных сторон многоугольников ABCDE и abcde. Так как, сверх того, у этих многоугольников равны соответственные углы (как образованные параллельными и одинаково направленными сторонами), то они подобны.

3) Площади подобиях многоугольников относятся как квадраты сходственных сторон; поэтому 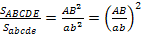. Но 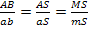, Значит, ■

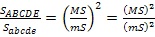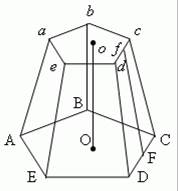
Если провести сечение abcde, параллельное основанию ABCDE пирамиды, то тело, заключённое между этими плоскостями и боковой поверхностью, называется усеченной пирамидой. Параллельные грани ABCDE и abcde называются основаниями; расстояние Oo между ними – высотой. Усечённая пирамида называется правильной, если пирамида, из которой она была получена – правильная. Все боковые грани правильной усечённой пирамиды – равные равнобочные трапеции. Высота Ff боковой грани называется апофемой правильной усечённой пирамиды.

Следствие из теоремы (*). У правильной усечённой пирамиды верхнее основание есть правильный многоугольник, подобный нижнему основанию, а боковые грани есть равные и равнобочные трапеции.

Доказательство: самостоятельно

Теорема: Боковая поверхность правильной усеченной пирамиды равна произведению полусуммы периметров обоих оснований на апофему

Доказательство: самостоятельно

Объем призмы и пирамиды

Два многогранника называются смежными, если они имеют одну или несколько общих граней и остальные точки многогранников расположены по разные стороны от их общих граней.

Если в двух данных смежных многогранниках не рассматривать их общих граней, то образуется третий многогранник, называемый их суммой.

Определить объем многогранника – значит поставить в соответствие любому многограннику положительное число, называемое его объемом, и обладающее следующими свойствами:

1. Кубу с ребром равным единице длины соответствует объем равный единице объема

2. Равные тела имеют равные объёмы.

3. Объём многогранника представляющего собой сумму многогранников (Р и Q), равен сумме объёмов этих многоранников.

Два тела, имеющие одинаковые объемы, называются равновеликими.

⇐ Предыдущая 123 Следующая ⇒