Лекция 6. Многогранники. Призма

Лекция 6

Многогранники

Многогранник – это тело, граница которого состоит из кусков плоскостей (многоугольников). Эти многоугольники называются гранями, их стороны – рёбрами, их вершины – вершинамимногогранника. Отрезки, соединяющие две вершины и не лежащие на одной грани, называются диагоналямимногогранника.

Многогранник – выпуклый, если все его диагонали расположены внутри него.

Призма

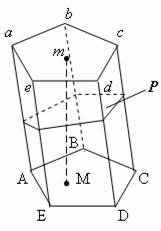
Призма – это многогранник, две грани которого ABCDE и abcde ( основания призмы ) – равные многоугольники с соответственно параллельными сторонами, а остальные грани ( AabB, BbcC и т.д.) - параллелограммы, плоскости которых параллельны прямой ( Aa, или Bb, или Cc и т.д. ). Параллелограммы AabB, BbcC и т.д. называются боковымигранями; рёбра Aa, Bb, Cc и т.д. называются боковымирёбрами. Высота призмы – это любой перпендикуляр, опущенный из любой точки основания на плоскость другого основания. В зависимости от формы многоугольника, лежащего в основании, призма может быть соответственно: треугольной, четырёхугольной, пятиугольной, шестиугольной и т.д.

Если боковые рёбра призмы перпендикулярны к плоскости основания, то такая призма называется прямой; в противном случае – это наклонная призма. Если в основании прямой призмы лежит правильный многоугольник, то такая призма также называется правильной.

Нормальное (ортогональное, перпендикулярное) сечение Р призмы – это сечение, образованное плоскостью, перпендикулярной боковому ребру.

Теорема: Боковая поверхность призмы равна произведению бокового ребра на периметр ортогонального сечения

Доказательство: самостоятельно

Параллелепипед - это призма, основания которой параллелограммы. Таким образом, параллелепипед имеет шесть граней и все они – параллелограммы. Противоположные грани попарно равны и параллельны.

Если четыре боковые грани параллелепипеда – прямоугольники, то он называется прямым. Прямой параллелепипед, у которого все шесть граней – прямоугольники, называется прямоугольным.

Теорема: Диагональ прямоугольного параллелепипеда d и его рёбра a, b, c связаны соотношением: d²= a²+ b² + c².

Доказательство: самостоятельно

Прямоугольный параллелепипед, все грани которого квадраты, называется кубом. Все рёбра куба равны.

12 3 Следующая ⇒