ЗАДАНИЯ для самостоятельного решения

(10)

(плоскости не могут быть параллельны, т.е. коэффициенты A₁, B₁, C₁ не могут быть пропорциональны коэффициентам A₂, B₂, C₂). Система уравнений (10) называются общим уравнением прямой в пространстве.

В связи со сказанным выше определить прямые, как раньше, не удается. Единственным видом уравнения прямой, совпадающим и на плоскости, и в пространстве, является параметрическое уравнение прямой.

Рассмотрим прямую на плоскости. Если заданы точка 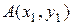, лежащая на прямой, и 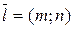- направляющий вектор прямой (т.е. вектор, параллельный прямой), то параметрическое уравнение прямой имеет вид

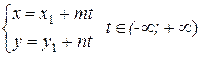, (11)

В пространстве же получаем

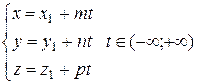, (12)

где, как и ранее, 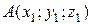– точка, лежащая на прямой, а 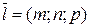- направляющий вектор прямой.

Пример 8. Для прямой, заданной параметрическим уравнением 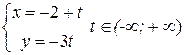, выписать направляющий вектор, координаты двух точек, лежащих на прямой, координаты вектора нормали и угловой коэффициент.

Решение. В соответствии с (11) 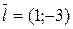(его координаты – коэффициенты при параметре t, а точка A(-2;0) лежит на прямой. Чтобы найти координаты второй точки, лежащей на прямой, зададим какое-нибудь значение параметра t. В частности, при t=1 x=-1, y=-3, т.е. точка B(-1;-3) принадлежит прямой.

Вектор нормали связан с общим уравнением прямой, а чтобы перейти к нему, необходимо в одном из заданных уравнений выразить t через x и полученное выражение подставить во второе уравнение. Например, из первого уравнения 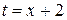, поэтому 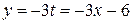. Далее, 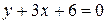и .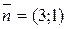

Наконец, для определения углового коэффициента выражаем y: 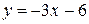. Отсюда .

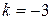Пример 9. Записать параметрическое уравнение прямой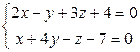

При решении такой задачи одну из переменных можно выбрать параметром, а оставшиеся выразить через нее, решая систему уравнений. Например, в данной задаче в качестве параметра выберем t, т.е. положим t=y. Система принимает вид 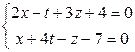. Исключим из системы переменную х, вычитая из первого уравнения два вторых: 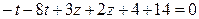, , 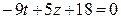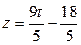. Аналогично исключаем переменную z, прибавляя к первому уравнению три вторых: 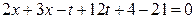, , 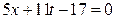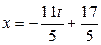. Итак, 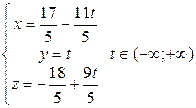. Для проверки можно найти координаты пары точек (задавая значения параметра) и убедиться, что они удовлетворяют исходной системе.

Пример 10. Написать параметрическое и общее уравнения прямой, проходящей через точки A(-1;2;4) и B(2;5;3).

Решение.Начнём с параметрического.В качестве точки, лежащей на плоскости, можно взять любую из заданных; пусть, для определенности, это будет точка A. Направляющим вектором прямой является вектор :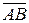

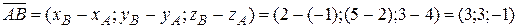Таким образом, 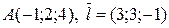и в силу (2.3б) параметрические уравнения имеют вид .

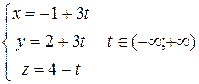Чтобы составить общее уравнение, необходимо из одного из параметрических уравнений выразить t и подставить полученное выражение в оставшиеся уравнения. Например, в данном примере из третьего уравнения получаем t=4-z, и поэтому 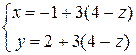или окончательно .

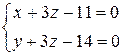Замечание. При составлениипараметрического уравнения можно было в качестве направляющего вектора взять 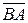, а в качестве лежащей на прямой точки – B. Вы можете получить 4 различных вида параметрического уравнения прямой.

ЗАДАНИЯ для самостоятельного решения

Упражнение 1. Для прямых, заданных уравнениями в общем виде, выписать вектор нормали, определить угловой коэффициент, построить прямые:

⇐ Предыдущая 123 Следующая ⇒