
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Обратите внимание, что и (8), и (***) – верные! Хотя в первом вычитаются координаты второй точки, а во втором – первой.
1.Прямая на плоскости.Среди различных уравнений прямой на плоскости наиболее распространенными можно считать следующие.
Общее уравнение прямой на плоскости имеет вид
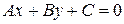 ,
, 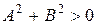 (1)
(1)
где A, B, C – вещественные числа (неравенство 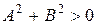 означает, что коэффициенты A и B не обращаются в нуль одновременно). Вектор
означает, что коэффициенты A и B не обращаются в нуль одновременно). Вектор 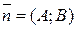 называется вектором нормали и перпендикулярен данной прямой.
называется вектором нормали и перпендикулярен данной прямой.
Частными случаями являются уравнения 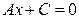 и
и 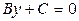 . Первое из них после деления на коэффициент A, не равный 0, превращается в уравнение
. Первое из них после деления на коэффициент A, не равный 0, превращается в уравнение 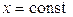 и задает прямую, параллельную оси ОУ, второе – в уравнение
и задает прямую, параллельную оси ОУ, второе – в уравнение 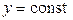 , задающее прямую, параллельную оси ОХ.
, задающее прямую, параллельную оси ОХ.
Уравнение прямой с угловым коэффициентом представляет собой уравнение, разрешенное относительно y:
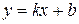 . (2)
. (2)
Здесь вещественное число b – это ордината точки пересечения прямой и оси OY, вещественное число k – это угловой коэффициент прямой (тангенс угла, который прямая образует с положительным направлением оси OX). При k=0 получается уравнение прямой 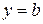 , проходящей через точку с координатами (0;b) параллельно оси OX (при b=0 это уравнение самой оси OX
, проходящей через точку с координатами (0;b) параллельно оси OX (при b=0 это уравнение самой оси OX 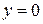 ), при k>0 прямая образует с осью OX острый угол, при k<0 – тупой.
), при k>0 прямая образует с осью OX острый угол, при k<0 – тупой.
Замечание. Следует отдельно рассмотреть прямую, заданную уравнением x=a (a – вещественное число). Она проходит через точку с координатами (a;0) параллельно оси OY ( при a=0 получаемуравнение оси OY) и образует с осью OX угол в 900. Угловой коэффициент такой прямой не определен!
Уравнение прямой в отрезках записывается в виде
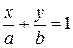 , (3)
, (3)
где a и b – соответствующие координаты точек пересечения прямой с осью OX (точка A(a;0)) и OY (точка B(0;b)). Например, прямая 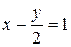 проходит через точки A(1;0) и B(0;-2); прямая
проходит через точки A(1;0) и B(0;-2); прямая 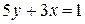 через точки A(1/3;0) и B(0;1/5) (так как уравнение
через точки A(1/3;0) и B(0;1/5) (так как уравнение 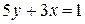 равносильно уравнению
равносильно уравнению 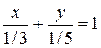 ).
).
Пример 1. Дана прямая 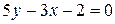 . 1) Выписать ее вектор нормали.
. 1) Выписать ее вектор нормали.
2) Найти угловой коэффициент, построить прямую на плоскости. 3) Привести уравнение прямой к виду «уравнение в отрезках, сравнить с результатом построения в 2).
Решение. 1) Сравнивая уравнение данной прямой с (1), замечаем, что в нашем случае 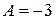 (коэффициент при x),
(коэффициент при x), 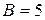 (коэффициент при y), поэтому
(коэффициент при y), поэтому 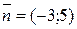 .
.
2) Чтобы найти угловой коэффициент, исходное уравнение необходимо разрешить относительно y: 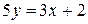 и
и 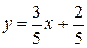 . Сравнивая последнее уравнение с уравнением (2), замечаем, что k=3/5. Как известно, для построения прямой необходимо знать координаты двух точек, через которые проходит прямая. Задавая значения x в
. Сравнивая последнее уравнение с уравнением (2), замечаем, что k=3/5. Как известно, для построения прямой необходимо знать координаты двух точек, через которые проходит прямая. Задавая значения x в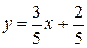 , можно найти соответствующие значения y:
, можно найти соответствующие значения y: 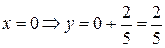 ;
; 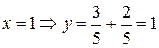 . Итак, остается провести прямую, проходящую через точки В(0; 2/5), М(1; 1).
. Итак, остается провести прямую, проходящую через точки В(0; 2/5), М(1; 1).
3) Уравнение 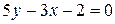 равносильно уравнению
равносильно уравнению 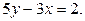 Разделим обе части уравнения на 2 (чтобы справа получить 1):
Разделим обе части уравнения на 2 (чтобы справа получить 1): 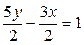 . Приведем уравнение к виду (3), отправив числа из числителей дробей в «знаменатель знаменателя» и включив «-» в знаменатель второй дроби:
. Приведем уравнение к виду (3), отправив числа из числителей дробей в «знаменатель знаменателя» и включив «-» в знаменатель второй дроби:  (в принципе, можно еще и слагаемые расположить в «правильном», соответствующем (3), порядке:
(в принципе, можно еще и слагаемые расположить в «правильном», соответствующем (3), порядке: 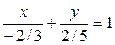 ). Итак,
). Итак, 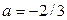 ,
, 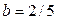 . Прямая проходит через точки А(-2/3;0), В(0; 2/5).
. Прямая проходит через точки А(-2/3;0), В(0; 2/5).
2. Угол j между прямыми. Если прямые заданы уравнениями с угловым коэффициентом ( 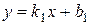 ,
, 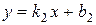 ), то угол между ними определяется с помощью формулы
), то угол между ними определяется с помощью формулы
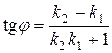 . (4)
. (4)
Из (4) вытекают условия параллельности( 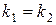 ) иперпендикулярности двух прямых (
) иперпендикулярности двух прямых ( 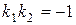 или
или 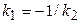 ).
).
Пример 2. Выбрать из прямых (I) – (V) параллельные и перпендикулярные, определить угол между прямыми (I) и (VI):
(I) 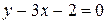 ; (II)
; (II) 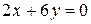 ; (III)
; (III)  ;
;
(IV) 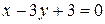 ; (V)
; (V) 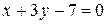 ; (VI)
; (VI) 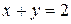 .
.
Решение. Сначала для каждой прямой найдем угловой коэффициент:
(I): 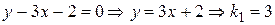 ;
;
(II): 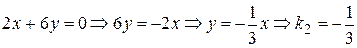 ;
;
(III) 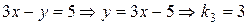 ;
;
(IV) 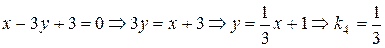 ;
;
(V) 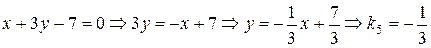 ;
;
(VI) 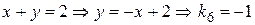 .
.
Поскольку 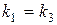 ,
, 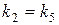 , получаем, что прямые (I) и (III), (II) и (V) параллельны. С другой стороны,
, получаем, что прямые (I) и (III), (II) и (V) параллельны. С другой стороны, 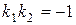 , а потому прямые (I) и (II) перпендикулярны (значит, перпендикулярны и прямые (III) и (II), (I) и (V), (III) и (V)).
, а потому прямые (I) и (II) перпендикулярны (значит, перпендикулярны и прямые (III) и (II), (I) и (V), (III) и (V)).
Чтобы найти тангенс угла между прямыми (I) и (VI), воспользуемся формулой (4): 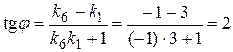 . Но тогда
. Но тогда 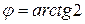 .
.
ЗАМЕЧАНИЕ 1 (о знаке найденного тангенса).
ЗАМЕЧАНИЕ 2 (о точке пересечения прямых). Если точка лежит на прямой, то её координаты должны удовлетворять уравнению прямой. Точка пересечения прямых – это точка, удовлетворяющая всем уравнениям прямых, которые в ней пересекаются. Значит, чтобы найти её координаты, необходимо решить систему соответствующих уравнений. При этом можно использовать метод исключения неизвестных, изученные ранее методы решения систем линейных алгебраических уравнений или, выразив одно из неизвестных через другое в любом уравнении, подставить полученное выражение в оставшееся уравнение.
Пример 3. Найти точку пересечения прямых 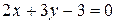 и
и 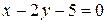 .
.
Решение. Рассмотрим систему уравнений 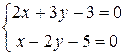 . Из второго уравнения
. Из второго уравнения 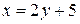 , подставляем полученное выражение в первое уравнение:
, подставляем полученное выражение в первое уравнение: 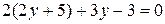 ,
, 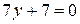 ,
, 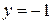 . Возвращаемся к выражению для
. Возвращаемся к выражению для 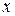 :
: 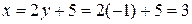 . Итак, точка пересечения заданных прямых – А(3;-1).
. Итак, точка пересечения заданных прямых – А(3;-1).
3. Составление уравнений прямых на плоскости. Рассмотрим основные типы возникающих задач.
1) Записать уравнение прямой с известным угловым коэффициентом 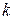 , проходящей через заданную точку
, проходящей через заданную точку  . Ответом является уравнение
. Ответом является уравнение
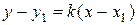 . (5)
. (5)

2) Записать уравнение прямой, проходящей через точку 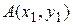 параллельно прямой
параллельно прямой 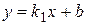 . Для решения используем уравнение (5) и учтем, что угловые коэффициенты параллельных прямых совпадают:
. Для решения используем уравнение (5) и учтем, что угловые коэффициенты параллельных прямых совпадают:
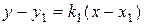 . (6)
. (6)
3) Записать уравнение прямой, проходящей через точку 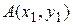 перпендикулярно прямой
перпендикулярно прямой 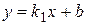 . Угловые коэффициенты перпендикулярных прямых связаны соотношением
. Угловые коэффициенты перпендикулярных прямых связаны соотношением 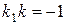 , поэтому
, поэтому  . Остается подставить это в (5) и получить уравнение:
. Остается подставить это в (5) и получить уравнение:
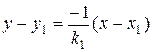 . (7)
. (7)
4) Уравнение прямой, проходящей через две заданные точки  ,
,  , имеет вид
, имеет вид
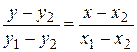 . (8)
. (8)

Обратите внимание, что и (8), и (***) – верные! Хотя в первом вычитаются координаты второй точки, а во втором – первой.
Пример 4. Составить уравнение прямой, проходящей через точку A(2,-3) и образующей с положительным направлением оси OX угол 1200.
Решение. Координаты точки известны, а угловой коэффициент 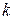 - это тангенс угла наклона, т.е.
- это тангенс угла наклона, т.е.  . Подставляя в (5), получаем:
. Подставляя в (5), получаем: 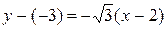 или
или 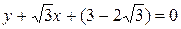 .
.
Пример 5. Составить уравнения прямых, проходящих через точку
A(2,-3) параллельно и перпендикулярно прямой 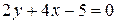 .
.
Решение. Так как 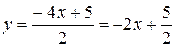 , то угловой коэффициента данной прямой
, то угловой коэффициента данной прямой 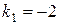 . Чтобы составить уравнение параллельной прямой, проходящей через A(2,-3), воспользуемся (6):
. Чтобы составить уравнение параллельной прямой, проходящей через A(2,-3), воспользуемся (6): 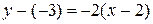 или
или 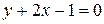 . Результат можно проверить, подставив в полученное выражение координаты заданной точки:
. Результат можно проверить, подставив в полученное выражение координаты заданной точки: 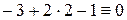 (получили тождество, значит, всё верно).
(получили тождество, значит, всё верно).
Аналогично действуем при составлении уравнения перпендикулярной прямой, только используем (7): 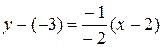 ,
, 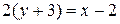 , и окончательно
, и окончательно 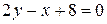 . Проверка:
. Проверка: 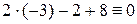 .
.
Пример 6. Написать уравнение прямой, проходящей через точки A(3;7), B(-1;5).
Решение.Подставляя в (8) координаты данных точек, получаем:
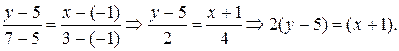
Собирая теперь всё в одну сторону, приходим к уравнению 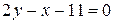 (проверьте справедливость уравнения, как это сделано в примере 5!).
(проверьте справедливость уравнения, как это сделано в примере 5!).
Пример 7. В треугольнике с вершинами O(0;0), A(3;3), B(-1;5): 1) найти уравнения стороны AB, медианы AE и высоты OК. 2) Найти длину этой высоты.
Решение. Уравнение стороны AB составляем, используя формулу (8): 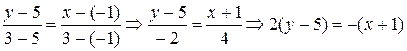 , откуда
, откуда 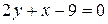 .
.
Далее, по определению медианы треугольника точка E – середина отрезка BO, поэтому ее координаты можно найти по формуле «полусумма соответствующих координат», поэтому
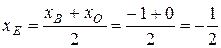 ,
, 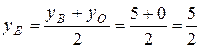 .
.
Таким образом, теперь надо составить уравнение прямой, проходящей через точки A(3;3) и E(-1/2;5/2). Подставляем их координаты в (8):
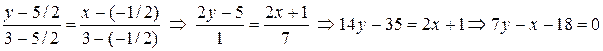 .
.
Итак, уравнение медианы AE имеет вид 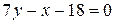 .
.
Высота OK – это прямая, проходящая через вершину O перпендикулярно прямой AB. Воспользуемся уравнением (7). Угловой коэффициент 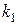 прямой AB находим из уравнения
прямой AB находим из уравнения 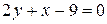 :
: 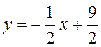 , поэтому
, поэтому 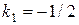 . Тогда имеем:
. Тогда имеем: 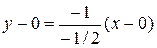 , и уравнение высоты OK
, и уравнение высоты OK 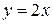 .
.
2) Найдем координаты K – точки пересечения построенной высоты и прямой AB. Решаем систему уравнений: 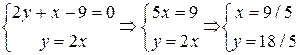 . Итак,
. Итак, 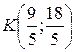 , и тогд
, и тогд 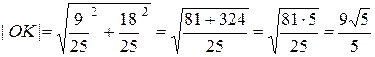 .
.
4. Уравнения прямой и плоскости в пространстве. В пространстве уравнение
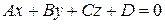 (
( 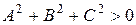 ) (9)
) (9)
задает плоскость, при этом вектор 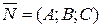 перпендикулярен рассматриваемой плоскости и называется вектором нормали.
перпендикулярен рассматриваемой плоскости и называется вектором нормали.
Прямая в пространстве определяется как пересечение двух плоскостей:
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|