Экстремумы функций. Точка х = а называется точкой минимума функции у(х), если для всех х из некоторой окрестности точки а выполнено неравенство у(х) ≥ у(а). При этом значение у(а) называется минимумом функции у(х).. Точка х= а называется точкой ма

3. Экстремумы функций

При исследовании поведения функции вблизи некоторой точки х = а удобно пользоваться понятием окрестности этой точки. Окрестностью точки а называют любой интервал, содержащий эту точку.

Например, интервалы (3; 10), (4; 6), (4,8; 5,1) - некоторые окрестности точки а = 5.

Характерным свойством функции у(х) являются точки экстремума -точки, вкоторых меняется монотонностьфункции. При этом, если возрастаниефункции сменяетсяее убыванием,то такая точка о - точка максимума.Если, наоборот, убываниефункции сменяетсяее возрастанием,то такая точка b - точка минимума.Дадим более точное определение точек экстремума.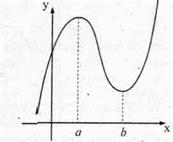

Точка х = а называется точкой минимума функции у(х), если для всех х из некоторой окрестности точки а выполнено неравенство у(х) ≥ у(а). При этом значение у(а) называется минимумом функции у(х).

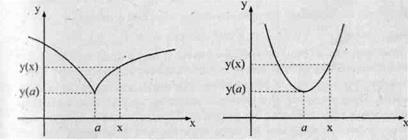
В простейших случаях легко найти точку минимума и минимум функции.

Пример 6. Для функции у = Х² + 6х +10 выделим полный квадрат суммы:

г = х² + 6х +10 = (х² + 6х + 9) +1 = 1 + (х + 3)². Так как при всех значениях х величина (х + 3)² >0, то данная функция имеет минимум у_min = 1 при условии

х + 3 = 0, то есть в точке минимума x_min = -3.

Точка х= а называется точкой максимума функции у(х), если для всех х из некоторой окрестности точки а выполнено неравенство у(х) < у(а). При этом значение у(а) называется максимумом функции у(х).

II. Решите упражнения на закрепление темы.

№ 77(а)

([-7;-5], [1;5] – возрастает; [-5;1] – убывает; точки max: -5, 5; точка min: 1; экстремумы: 5, -3, 3)

№82 (а)

(найти вершину параболы, сделать чертеж и по нему найти промежутки возрастания, убывания, точки максимума, точки минимума и экстремумы)

III. Домашнее задание: Колмогоров А.Н. Алгебра 10-11. § 2, пункт 5 (стр. 39-44)

⇐ Предыдущая 1 23