Монотонность тригонометрических функций

Пример 3

Исследуем на монотонность функцию у =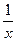

Область определения данной функции - промежутки (-∞; 0) и (0; ∞). График этой функции (гипербола) хорошо известен.

Видно, что функция убывает в области определения. Исследуем ее на

монотонность. Выберем точки х₁ и х₂ из области определения, так что х₂ > х₁. Найдем разность у(х₂) - у(х₁) = 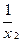- 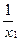= 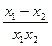. Так как х₂>х₁, то числитель этой дроби отрицательный. Если х₁ и х₂ лежат в одном промежутке области определения (то есть х_1,х₂ < 0 или х_1. х₂>0, то произведение х₁ • х₂> 0. Поэтому дробь отрицательна, то есть у(х₂) - у(х₁) < 0 или у(х₂) < у(х₁). В итоге получаем правильный результат - функция является убывающей.

Если х₁ и х₂ лежат в разных промежутках области определения (то есть х₁ < 0 и х₂ > 0), то произведение х₁х₂< 0. Поэтому дробь положительна, то есть у(х₂) - у(х₁) > 0 или у(х₂) < у(х₁). В результате получаемгрубую ошибку - функция является возрастающей.

2. Монотонность тригонометрических функций

Так как графики основных тригонометрических функций известны, то по ним легко установить их монотонность.

Пример 4

Докажем, что функция у = cos х убывает на промежутках [2πn; π +2πn].

Понятно, что в силу периодичности косинуса достаточно доказать утверждение для промежутка [0; π]. Используя определение убывающей функции и формулу разности косинусов, получим:

У(х₂) - у(х₁) = cos х₂ - cos х, = -2 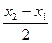sin sin 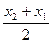. Определим

знак этого выражения, найдя знак каждого множителя. Из неравенства 0 ≤ х₁ < х₂ ≤ л можно получить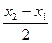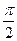: 0< ≤ и 0 < <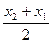

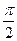
Поэтому sin 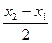>0 и sin 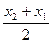>0. Следовательно, данное про-

изведение отрицательно, то есть у(х₂) - у(х₁) < О или у(х₂)-^<у(х₁). Таким образом, на указанных промежутках функция у = cos х убывает.

⇐ Предыдущая 123 Следующая ⇒