ХОД УРОКА.. I. Изучение нового материала.. Функции называется убывающей, если большему значению функции соответствует меньшее значение аргумента. если х2 > х1, то f(x2 ) < f(x1))

ТЕМА УРОКА: «Возрастание и убывание функции. Экстремумы».

ЦЕЛЬ: дать понятие монотонности промежутков возрастания и убывания, экстремумов функции.

ХОД УРОКА.

I. Изучение нового материала.

1. Монотонность функции.

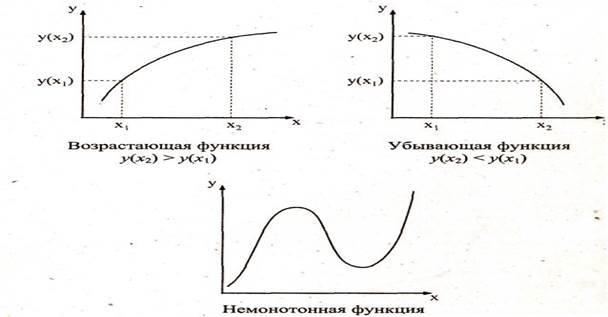
Рассмотрим еще одно свойство функции – монотонность (то есть возрастание и убывание). Функция называется возрастающей, если большему значению аргумента соответствует большее значение функции

(если х₂ > х₁, то f(x₂ ) > f(x₁))

Функции называется убывающей, если большему значению функции соответствует меньшее значение аргумента

(если х2 > х1, то f(x2 ) < f(x1))

(чертеж на доске графиков функций монотонно возрастающей и убывающей)

Пример 1. Определить монотонность функции: у(х) = -2х + 4. Область определения этой функции – все действительные числа. Возьмем два значения х из области определения этой функции х₁ и х₂ и пусть х₂> х₁. Найдем значение функции в этих точках: у(х₁) = - 2 х₁ + 4 и у(х₂) = - 2 х₂ + 4. Сравним эти значения и определим, какое из них больше. Для этогорассмотрим разницу этих величин: у(х₂) - у(х₁) = ( - 2 х₂ +4) – ( - 2 х₁ +4) =

= - 2 х₂+ 4 + 2 х₁ – 4 = - 2 (х₂ - х₁ )

Данная функция является убывающей (чертеж графика на доске).

Функция по всей области определения может быть немонотонна, но на отдельных промежутках функция может быть монотонной. Например. Функция у = - х³ +6х -8 в целом не монотонна, но на промежутке (3; ∞) функция убывает, а на промежутке ( - ∞; 3) – возрастает. Соответственно такие промежутки называются промежутками возрастания и убывания.

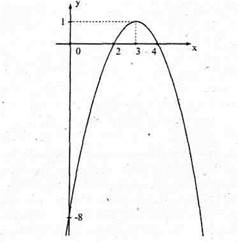
Пример 2. Область определения функции у = - х² +6х – 8 является

D(y) = ( - ∞; ∞). Возьмем два значения х из области определения х₁ и х_г и пусть х₂ > х₁. Найдем значения функции в этих точках: у(х₁) = - х₁²+ 6 х₁ -8 и у(х₂) = - х₂² + 6х₂ - 8 . Сравним эти значения. Рассмотрим разность этих величин У(х₂)-У(х₁) = - х₂²+ х₁² +6 х₂ - 6 х₁ = (х₂ - х₁)( х₂+ х₁) + 6(х₂ - х₁) =

= (х₂ - х₁)(6 - х₂ - х₁). Первый множитель в этом произведении положительный, так как х₂ > х₁ по договоренности. Второй же множитель может иметь разный знак. Рассмотрим два случая.

а) Пусть х₁ < х₂ ≤ 3, Тогда х₁+ х₂ < 6 и второй множитель 6 - х₁ - х₂ > 0. Поэтому произведение положительно и у(х₂) - у(х₁) > 0 , то есть

у(х₂) > у(х₁). Следовательно, функция у(х) возрастает на промежутке (-∞;3]. б) Пусть х₂ > х₁≥ 3, тогда х₁ + х₂ > 6 и второй множитель 6 - х₁ - х₂ < 0. Поэтому произведение отрицательно и у(х₂) - у(х₁) < 0, то есть у(х₂) <у( х₁). Следовательно, функция у(х) убывает на промежутке [3; ∞).

Из данного графика видны промежутки возрастания и убывания.

Если область определения функции состоит из нескольких промежутков, то при исследовании функции на монотонность надо выбирать точки х₁ и х₂ , лежащие в одном промежутке.

12 3 Следующая ⇒