Евклидово пространство

2. Евклидово пространство

Введем в линейном (векторном) пространстве метрику, т.е. способ измерения длин и углов. Это можно сделать, если ввести, например, понятие скалярного произведения (аналогично тому, как это было сделано в п.1).

Определение 1. Скалярным произведением двух векторов 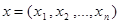и 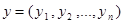называется число

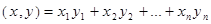Определение 2.Евклидовым пространством называется векторное (линейное) пространство, в котором задано скалярное произведение векторов, удовлетворяющее следующим свойствам:

1) (x,y)=(y,x)

2) (x,y+z)=(x,y)+(x,z)

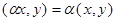
4) 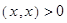, если ;

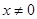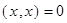, если .

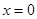Определение 3. Длиной (нормой) вектора x в евклидовом пространстве называется корень квадратный из его скалярного квадрата:

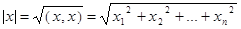
Свойства длины вектора:

1. ,

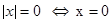2. 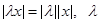– действительное число,

3. 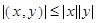– неравенство Коши–Буняковского,

4. 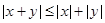– неравенство треугольника.

Угол между двумя векторами x и y определяется равенством (из свойства 3)

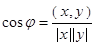где .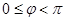

Определение 4. Два вектора называются ортогональными, если их скалярное произведение равно 0.

Векторы 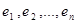n-мерного евклидова пространства образуют ортогональный базис, если эти векторы попарно ортогональны, т.е. 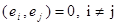, ортонормированный базис, если эти векторы попарно ортогональны и норма (длина) каждого из них равна единице, т.е. ;

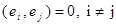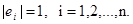
Теорема. Во всяком n-мерном евклидовом пространстве существует ортонормированный базис.

Пример ортонормированного базиса в n-мерном евклидовом пространстве – система единичных векторов .

Ортогональные и ортонормированные базисы играют в линейной алгебре роль, аналогичную прямоугольной (декартовой) системе координат в аналитической геометрии.

⇐ Предыдущая 1 23