
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задание 12 № 71243. Решение.. Задание 13 № 513092. Решение.. Задание 14 № 521354. Решение.. Задание 15 № 511560. Решение.. Задание 16 № 505176. Решение.. Задание 17 № 517456. Решение.. Задание 18 № 505988. Решение.. Примечение РЕШУ ЕГЭ.
12. Задание 12 № 71243
Найдите наибольшее значение функции 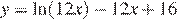 на отрезке
на отрезке 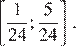
Решение.
Найдем производную заданной функции:
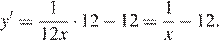
Найдем нули производной на заданном отрезке:
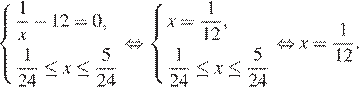
Определим знаки производной функции на заданном отрезке и изобразим на рисунке поведение функции:
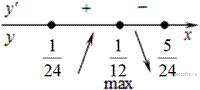
В точке 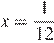 заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:
заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:

Ответ: 15.
13. Задание 13 № 513092
а) Решите уравнение 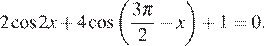
б) Найдите все корни этого уравнения, принадлежащие промежутку 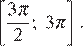
Решение.
а) Имеем:
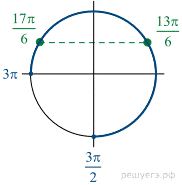
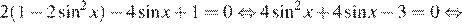
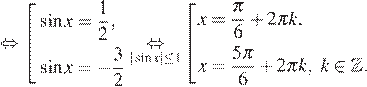
б) На указанном промежутке лежат точки 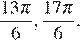
Ответ: а) 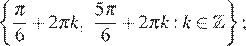 б)
б) 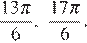
14. Задание 14 № 521354
Дана прямая призма АВСA1B1C1.
а) Докажите, что линия пересечения плоскостей АВС1 и А1В1С параллельна основаниям призмы.
б) Найдите угол между плоскостями АВС1 и А1В1С, если известно, что АС = 1, ВС = 2, АВ =  , СС1 = 3.
, СС1 = 3.
Решение.
а) Пусть O — точка пересечения A1C и AC1. Проведем через нее прямую, параллельную AB и A1B1. Очевидно, она лежит в обеих плоскостях. Поэтому она-то и есть линия их пересечения. Она параллельна AB, поэтому параллельна плоскости основания призмы.
б) Поскольку 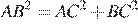 , треугольник ABC — прямоугольный. Введем координаты с началом в точке C и с осями x, y, z, направленными вдоль ребер CA, CB, CC1 соответственно. Тогда координаты точек будут
, треугольник ABC — прямоугольный. Введем координаты с началом в точке C и с осями x, y, z, направленными вдоль ребер CA, CB, CC1 соответственно. Тогда координаты точек будут
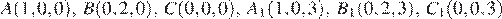 .
.
Уравнение плоскости ABC1 будет 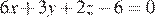 , уравнение плоскости A1B1C будет
, уравнение плоскости A1B1C будет 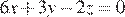 , и
, и 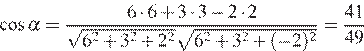 .
.
Ответ 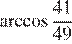 .
.
15. Задание 15 № 511560
Решите неравенство: 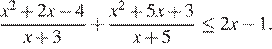
Решение.
Имеем:
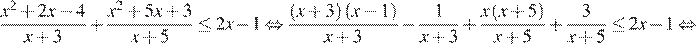
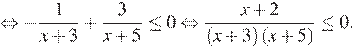
Применяя метод интервалов, получаем: 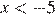 или
или 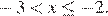
Ответ: 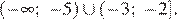
16. Задание 16 № 505176
На диагонали параллелограмма взяли точку, отличную от её середины. Из неё на все стороны параллелограмма (или их продолжения) опустили перпендикуляры.
а) Докажите, что четырёхугольник, образованный основаниями этих перпендикуляров, является трапецией.
б) Найдите площадь полученной трапеции, если площадь параллелограмма равна 24, а один из его углов равен 45°.
Решение.
 а) Возьмём на диагонали AC параллелограмма ABCD точку O (не посередине) и проведём через неё перпендикуляры NL и KM к сторонам параллелограмма (см. рис.). Прямоугольные треугольники CKO и AMO подобны.
а) Возьмём на диагонали AC параллелограмма ABCD точку O (не посередине) и проведём через неё перпендикуляры NL и KM к сторонам параллелограмма (см. рис.). Прямоугольные треугольники CKO и AMO подобны.
Точно так же подобны треугольники CNO и ALO:
OK : OM = OC : OA = ON : OL.
Отсюда следует подобие треугольников ONK и OLM. Тогда накрестлежащие углы OML и OKN равны, а поэтому прямые NK и ML параллельны. Следовательно, четырёхугольник KLMN — параллелограмм или трапеция.
Докажем, что это трапеция. Если KLMN — параллелограмм, то ON = OL.
В этом случае OC = OA, то есть O — середина AC. Противоречие. Значит, KLMN — трапеция.
б) Обозначим площадь параллелограмма S, а его острый угол — α. Угол между диагоналями NL и KM трапеции KLMN равен углу между перпендикулярными диагоналям прямыми BC и CD, то есть этот угол равен α.
Поэтому площадь трапеции равна:
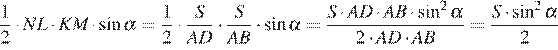
Подставляя α = 45° и S = 24, получаем, что площадь трапеции равна
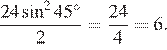
Ответ: 6.
17. Задание 17 № 517456
В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— Каждый январь долг увеличивается на r% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 77 760 руб, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 131 760 руб, то кредит будет полностью погашен за 2 года. Найдите r.
Решение.
Пусть сумма кредита S ежегодные выплаты x, 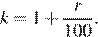 По условию долг на июль меняется так:
По условию долг на июль меняется так:
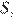
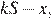
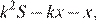
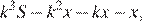
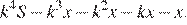
Если долг выплачен двумя равными платежами x2, то

Если долг выплачен четырьмя равными платежами x4, то
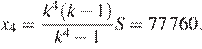
Тогда
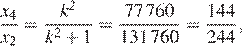
откуда 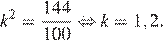 Следовательно,
Следовательно, 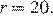
Ответ: 20.
18. Задание 18 № 505988
Найти все значения параметра 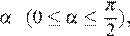 при каждом из которых наименьшее значение функции
при каждом из которых наименьшее значение функции 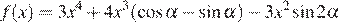 на отрезке
на отрезке 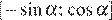 принимает наименьшее значение.
принимает наименьшее значение.
Решение.
Наименьшее значение эта функция принимает либо в нулях производной, либо в одном из концов отрезка. Найдем производную:
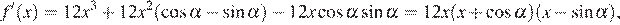
поэтому нули производной равны 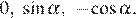
Если  то производная имеет вид
то производная имеет вид 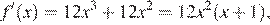 корни производной суть числа 0 и −1. Отрезок
корни производной суть числа 0 и −1. Отрезок 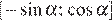 становится отрезком [0; 1], на нем функция f возрастает. Наименьшее значение достигается на левой границе отрезка. (*)
становится отрезком [0; 1], на нем функция f возрастает. Наименьшее значение достигается на левой границе отрезка. (*)
Если 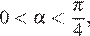 то
то  а
а 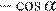 не лежит на отрезке
не лежит на отрезке 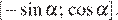 В этом случае имеем следующее расположение знаков производной:
В этом случае имеем следующее расположение знаков производной:
| Интервал | ( 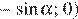
| 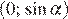
| ( 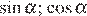 ) )
|
знак 
| + | − | + |
Наименьшего значения функция достигает либо на левой границе отрезка, либо в точке 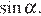 (**)
(**)
Если  то производная имеет вид
то производная имеет вид  Отрезок
Отрезок 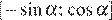 становится отрезком
становится отрезком 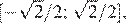 на нем функция лежит единственный корень производной — число 0. Это точка максимума, поэтому наименьшее значение достигается или на левой границе отрезка, или на правой границе. Эти значения равны, будем считать, что наименьшее значение достигается на левой границе (***).
на нем функция лежит единственный корень производной — число 0. Это точка максимума, поэтому наименьшее значение достигается или на левой границе отрезка, или на правой границе. Эти значения равны, будем считать, что наименьшее значение достигается на левой границе (***).
Объединяя случаи (*), (**) и (***) получаем, что если 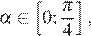 то ее наименьшее значение равно наименьшему из значений
то ее наименьшее значение равно наименьшему из значений 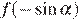 и
и 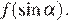 Имеем:
Имеем:
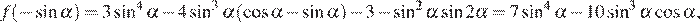

Рассмотрим разность найденных значений на отрезке 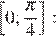
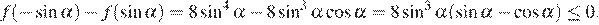
Поэтому
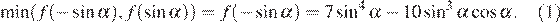
Если 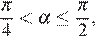 то
то 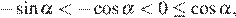 а
а 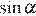 не лежит на указанном отрезке. Рассуждая аналогично, находим, что если
не лежит на указанном отрезке. Рассуждая аналогично, находим, что если 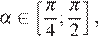 то функция убывает на
то функция убывает на 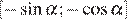 и на
и на 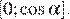 Проведя аналогичные вычисления, можно получить, что ее наименьшее значение равно
Проведя аналогичные вычисления, можно получить, что ее наименьшее значение равно
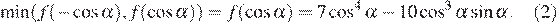
Осталось исследовать наименьшие значения (1) и (2) на соответствующих отрезках и найти наименьшее из них. Однако поскольку при замене 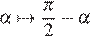 функции переходят друг в друга, достаточно будет исследовать одну из них. Иными словами, поскольку для всех α из отрезка
функции переходят друг в друга, достаточно будет исследовать одну из них. Иными словами, поскольку для всех α из отрезка 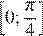 верно равенство
верно равенство 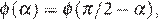 достаточно найти наименьшее значение функции
достаточно найти наименьшее значение функции 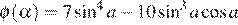 на промежутке
на промежутке 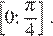
Исследуем производную функции на интервале 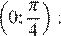
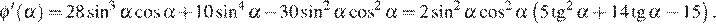
Решениями уравнения 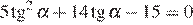 являются числа
являются числа 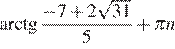 и
и 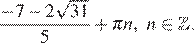 На интервале
На интервале 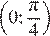 значения тангенса положительны и меньше 1, поэтому в него входит только корень
значения тангенса положительны и меньше 1, поэтому в него входит только корень 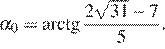
На интервале 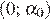 производная
производная 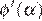 отрицательна, на интервале
отрицательна, на интервале 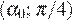 положительна. Следовательно, функция
положительна. Следовательно, функция 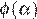 убывает на отрезке
убывает на отрезке 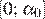 и возрастает на отрезке
и возрастает на отрезке 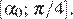 Поэтому наименьшее значение
Поэтому наименьшее значение 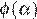 на отрезке
на отрезке 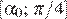 достигается в точке
достигается в точке 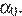 Такое же наименьшее значение
Такое же наименьшее значение 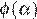 принимает и в точке
принимает и в точке 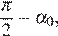 принадлежащей отрезку
принадлежащей отрезку 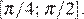
Итак, наименьшее значение достигается в точках 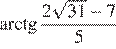 и
и 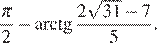
Примечение РЕШУ ЕГЭ.
Это задание из вступительного экзамена в Московский государственный университет несколько сложнее других.
19. Задание 19 № 485960
В возрастающей последовательности натуральных чисел каждые три последовательных члена образуют либо арифметическую, либо геометрическую прогрессию. Первый член последовательности равен 1, а последний 2076.
а) может ли в последовательности быть три члена?
б) может ли в последовательности быть четыре члена?
в) может ли в последовательности быть меньше 2076 членов?
Решение.
а) Нет, поскольку 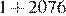 не делится на
не делится на 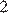 , а
, а 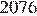 не является квадратом натурального числа.
не является квадратом натурального числа.
б) Последовательность не может быть арифметической прогрессией, поскольку 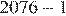 не делится на 3.
не делится на 3.
Последовательность не может быть геометрической прогрессией, поскольку 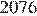 не является кубом натурального числа.
не является кубом натурального числа.
Если первые три члена образуют геометрическую прогрессию, а последние три – арифметическую, то эти числа:  но уравнение
но уравнение 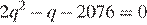 не имеет целых корней.
не имеет целых корней.
Если первые три члена образуют арифметическую прогрессию, а последние три – геометрическую, то эти числа: 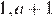 и
и 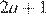 где
где 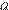 — натуральное число. Тогда последнее число должно равняться
— натуральное число. Тогда последнее число должно равняться
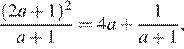
но это не натуральное число.
в) Да, например, 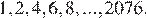
Ответ: а) Нет, б) нет, в) да.
Ключ
№ п/п
№ задания
Ответ
0,25
17,5
2,7
-367
0,648
а) 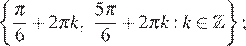 б)
б) 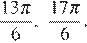
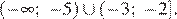
6.
20.
а) Нет, б) нет, в) да.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|