
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Физический смысл производной. Вычисление производной называется дифференцированием функции.. Правила дифференцирования. Таблица производных основных элементарных функций
§ 3. Физический смысл производной
Пусть с помощью закона s = s(t) задано прямолинейное неравномерное движение и t0 – время начала наблюдения. Средняя скорость движения 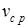 за время движения Dt, начиная с момента времени t0, определяется с помощью следующей формулы:
за время движения Dt, начиная с момента времени t0, определяется с помощью следующей формулы: 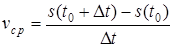 .
.
Нетрудно увидеть, что, по определению производной 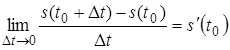 . С другой стороны,
. С другой стороны, 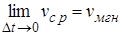 , где
, где 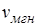 – мгновенная скорость в момент времени t0, то есть
– мгновенная скорость в момент времени t0, то есть 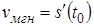 .
.
Таким образом, при прямолинейном неравномерном движении производная от функции, выражающей закон изменения пути от времени, равна мгновенной скорости движения точки.
Значение производной состоит в том, что при изучении любых процессов с её помощью можно оценить скорость изменения связанных между собой величин.
Вычисление производной называется дифференцированием функции.
§ 4. Правила дифференцирования
1) 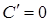 , где С – произвольная постоянная
, где С – произвольная постоянная
2) 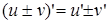 (Производная алгебраической суммы функций равна сумме(разности) производных этих же функций)
(Производная алгебраической суммы функций равна сумме(разности) производных этих же функций)
3) 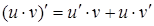
4) 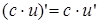 (Постоянная выносится за знак дифференцирования)
(Постоянная выносится за знак дифференцирования)
5) 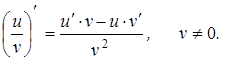
§ 5. Таблица производных основных элементарных функций
Производные от функции 
| Производные от сложной функции 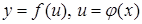
| |
| 1. |
| |
| Степенная функция | ||
| 2. | 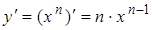
| 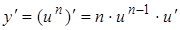
|
| Показательная функция | ||
| 3. | 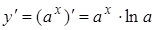
| 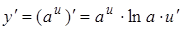
|
| 4. | 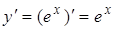
| 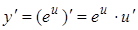
|
| Логарифмическая функция | ||
| 5. | 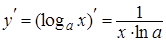
| 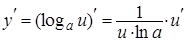
|
| 6. | 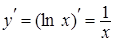
| 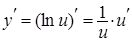
|
| Тригонометрические функции | ||
| 7. | 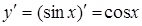
| 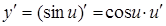
|
| 8. | 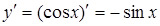
| 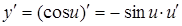
|
| 9. | 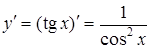
| 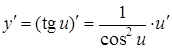
|
| 10. | 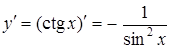
| 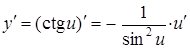
|
| Обратные тригонометрические функции | ||
| 11. | 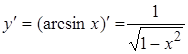
| 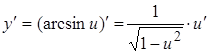
|
| 12. | 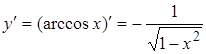
| 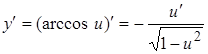
|
| 13. | 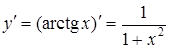
| 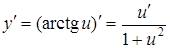
|
| 14. | 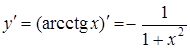
| 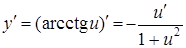
|
При дифференцировании степенной функции необходимо помнить:
1) 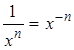 , например,
, например, 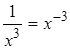
2) 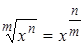 , например,
, например, 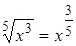
3) 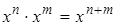 , например,
, например, 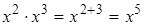
4) 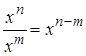 , например,
, например, 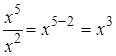
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
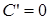 где С – произвольная постоянная
где С – произвольная постоянная