Хелпикс

Главная

Контакты

Случайная статья



Дифференциальное исчисление. функции одной переменной. Производная. Геометрический смысл производной. Производная функции в точке  равна тангенсу угла наклона касательной (к положительному направлению оси Ох), проведённой к графику функции в точке А( , ).

Стр 1 из 3Следующая ⇒


 

 

Дифференциальное исчисление

функции одной переменной

 

 Производная

    Пусть некоторая функция 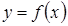 определена и непрерывна в некотором интервале (a, b) и 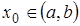. Рассмотрим произвольную точку 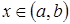. Обозначим разность 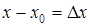. Dх будем называть приращением независимой переменной х. Разность  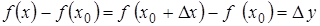будем называть приращением функции 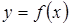, соответствующим приращению независимой переменной Dх (см. рис. 1). Так как х является переменной величиной, то и приращение Dх является переменной величиной (отметим, что, в силу произвольности выбора х, разность  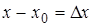может быть и отрицательной).

Определение 1. Если существует конечный предел отношения приращения функции к приращению аргумента 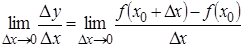, то он называется производнойфункции .

 

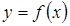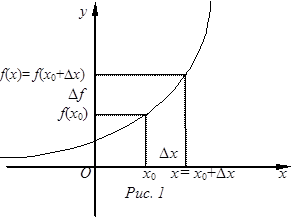
Обозначения: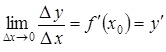  

 

Геометрический смысл производной

 Производная функции в точке  равна тангенсу угла наклона касательной (к положительному направлению оси Ох), проведённой к графику функции в точке А( , ).

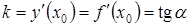
где α – угол между касательной к кривой в точке М(х0, y0) и положительным направлением оси Ох.

Уравнение касательной к кривой y = f(x)в точке М(х0, y0) имеет вид

 

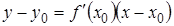
Пример

Найти уравнение касательной и нормали к кривой y = x3 + 2x в точке М(1, 3).

Решение:

Для определения углового коэффициента касательной находим производную от заданной функции: .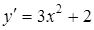

Вычислим угловой коэффициент касательной, подставив в производную абсциссу точки М(1, 3),имеем .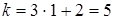

Таким образом, уравнение касательной имеет вид:

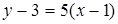; или ,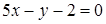

а уравнение нормали:

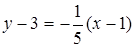, или .


123Следующая ⇒
  

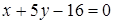© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.