Дисперсия

Дисперсия

Часто стандартное отклонение и дисперсию связывают вместе и делают это не без причины. Вот уравнение дисперсии, ничего не напоминает?

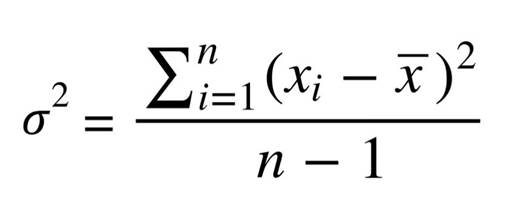
Дисперсия и стандартное отклонение — почти одно и то же! Дисперсия — просто квадрат стандартного отклонения. Более того, обе величины отражают одну и ту же вещь — меру разброса, хотя стоит отметить, что единицы измерения разные. В каких бы единицах ни измерялись ваши данные, единицы измерения отклонения будут такими же, а у дисперсии они будут возведены в квадрат.

Многие новички в статистике задают вопрос: «Зачем возводить отклонение в квадрат? Разве нельзя избавится от отрицательных слагаемых при помощи модуля?». Избавление от отрицательных значений — хорошая причина для возведения в квадрат, но не единственная. Как и на среднее значение, на дисперсию и стандартное отклонение влияют выбросы. Очень часто нас интересуют выбросы, поэтому возведение в квадрат позволяет выделить эту особенность. Если вы знакомы с математическим анализом, то поймете, что наличие экспоненциального выражения позволяет найти точку минимального отклонения.

Чаще всего при статистическом анализе нам понадобятся только среднее значение и стандартное отклонение, однако дисперсия по-прежнему важна в других академических областях. Меры центральной тенденции и разброса позволяют нам систематизировать данные и извлечь из них знания.

Ключевые идеи:

описательная статистика используется для систематизации и количественного описания данных;

среднее значение указывает на типичное значение в нашем наборе данных. Оно не робастно;

медиана является центральным значением в ряду данных. Она робастна;

мода — значение, которое появляется наиболее часто;

размах — это разность между максимальным и минимальным значениями в наборе данных;

дисперсия и стандартное отклонение являются средним расстоянием от среднего арифметического значения.

Задание № 1.
1. Используя Similar Datasets, провести описательную статистику любых 3 наборов, оформив отчет.

https://www.kaggle.com/zynicide/wine-reviews/data

⇐ Предыдущая 1 2 3 4 56