Элементы комбинаторики

1.3. Элементы комбинаторики

Для успешного решения задач с использованием классического определения вероятности необходимо знать основные правила и формулы комбинаторики - раздела математики, изучающего, в частности, методы решения комбинаторных задач - задач на подсчет числа различных комбинаций.

Пусть A_i (i = 1,2,...,n) - элементы конечного множества. Сформулируем два важных правила, часто применяемых при решении комбинаторных задач.

Правило суммы. Если элемент A₁ .может быть выбран n₁ способами, элемент A₂ - другими n₂ способами, A₃ - отличными от первых двух n₃ способами и т.д., A_K - n_k способами, отличными от первых (k - 1), то выбор одного из элементов: или A₁, или A₂,..., или A_k может быть осуществлен n₁+n₂+…+n_k способами.

Пример 1.8 В ящике 300 деталей. Известно, что 150 из них - 1-го сорта, 120 - 2-го, а остальные - 3-го сорта. Сколько существует способов извлечения из ящика одной детали 1-го или 2-го сорта?

Решение. Деталь 1-го сорта может быть извлечена n₁=150 способами, 2-го сорта – n₂=120 способами. По правилу суммы существует n₁+n₂= 150+120 = 270 способов извлечения одной детали 1-го или 2-го сорта.

Правило произведения. Если элемент A₁ .может быть выбран n₁ способами, после каждого такого выбора элемент A₂ может быть выбран n₂ способами и т.д., после каждого (k - 1) выбора элемент A_k может быть выбран n_k способами, то выбор всех элементов A₁, A₂,…, A_k указанном порядке может быть осуществлен n₁n₂…n_k способами.

Пример 1.9. В группе 30 человек. Необходимо выбрать старосту, его заместителя и профорга. Сколько существует способов это сделать?

Решение. Старостой может быть выбран любой из 30 учащихся, его заместителем - любой из оставшихся 29, а профоргом - любой из оставшихся 28 учащихся, т.е. n₁=30, n₂=29, n₃=28. По правилу произведения общее число способов выбора старосты, его заместителя и профорга равно n₁n₂n₃ = 30Ÿ29Ÿ28 =24360 способов.

Пусть дано множество из n различных элементов. Из этого множества могут быть образованы подмножества из m элементов (0£m£n). Например, из 5 элементов a, b, c, d, e могут быть отобраны комбинации по 2 элемента - ab, cd, eb, ba, ce и т.д., по 3 элемента - abc, cbd, cba, ead и т.д.

Если комбинации из n элементов по m отличаются либо составом элементов, либо порядком их расположения (либо и тем, и другим), то такие комбинации называют размещениями из n элементов по m. Число размещений из n элементов по m равно

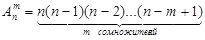(1.4)

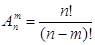или (1.5)

где n! равно произведению n первых чисел натурального ряда, т.е. n! = 1·2...n.

Пример 1.10 Расписание одного дня состоит из 5 уроков. Определить число вариантов расписания при выборе из 11 дисциплин.

Решение. Каждый вариант расписания представляет набор 5 дисциплин из 11, отличающийся от других вариантов как составом дисциплин, так и порядком их следования (или и тем, и другим), т.е. является размещением из 11 элементов по 5. Число вариантов расписаний, т.е. число размещений из 11 по 5, находим по формуле (1.4)

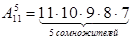=55440.

Если комбинации из n элементов по m отличаются только составом элементов, то их называют сочетаниями из n элементов по m. Число сочетаний из n элементов по m равно

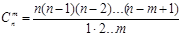(1.6)

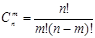или (1.7)

Так как по определению 0!=1, то 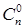= 1.

Свойства числа сочетаний:

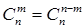(1.8)

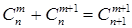(1.9)

Пример 1.11 В шахматном турнире участвуют 16 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна одна партия?

Решение. Каждая партия играется двумя участниками из 16 и отличается от других только составом пар участников, т.е. представляет собой сочетание из 16 элементов по 2. Их число находим по формуле (1.6):

=120

Если комбинации из n элементов отличаются только порядком расположения этих элементов, то их называют перестановками из n элементов. Число перестановок из n элементов равно

P_n=n! (1.10)

Пример 1.12 Порядок выступления 7 участников конкурса определяется жребием. Сколько различных вариантов жеребьевки при этом возможно?

Решение. Каждый вариант жеребьевки отличается только порядком участников конкурса, т.е. является перестановкой из 7 элементов. Их число по формуле (1.10): P₇ = 7! = 1×2×3×4×5×6×7 = 5040.

Если в размещениях (сочетаниях) из n элементов по m некоторые из элементов (или все) могут оказаться одинаковыми, то такие размещения (сочетания) называют размещением (сочетаниями) с повторениями из n элементов по m.

Например, из 5 элементов а, b, с, d, e по 3 размещениями с повторениями будут abc, cba, bcd, cdb, bbe, ebb, beb, ddd и т.д., сочетаниями с повторениями будут abc, bcd, bbe, ddd и т.д.

Число размещений с повторениями из n элементов по m равно

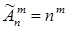(1.11)

а число сочетаний с повторениями из n элементов по m равно

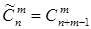(1.12)

где 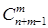определяется по формуле (1.6) или (1.7).

Пример 1.13 В конкурсе по 5 номинациям участвуют 10 кинофильмов. Сколько существует вариантов распределения призов, если по каждой номинации установлены: а) различные призы; б) одинаковые призы?

Решение. а) Каждый из вариантов распределения призов представляет собой комбинацию 5 фильмов из 10, отличающуюся от других комбинаций как составом фильмов, так и их порядком по номинациям (или и тем, и другим), причем одни и те же фильмы могут повторяться несколько раз, т.е. представляет размещение с повторениями из 10 элементов по 5. Их число по формуле (1.11) равно

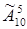=10⁵=100000.

б) Если по каждой номинации установлены одинаковые призы, то порядок следования фильмов в комбинации 5 призеров значения не имеет, и число вариантов распределения призов представляет собой число сочетаний с повторениями из 10 элементов по 5, определяемое по формуле (1.12) с учетом (1.6):

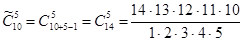=2002.

Если в перестановках из общего числа n элементов есть k различных элементов, при этом 1-й элемент повторяется n₁ раз, 2-й элемент – n₂ раз, k-й элемент – n_k раз, причем n₁+n₂+...+n_k=n, то такие перестановки называют перестановками с повторениями из n элементов. Число перестановок с повторениями из n элементов равно

P_n(n₁, n₂,…, n_k)= 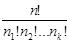(1.13)

Пример 1.14 Сколько существует семизначных чисел, состоящих из цифр 4,5 и 6, в которых цифра 4 повторяется 3 раза, а цифры 5 и 6 - по 2 раза?

Решение. Каждое семизначное число отличается от другого порядком следования цифр (причем n₁=3, n₂=2, n₃=2, а их сумма равна 7), т.е. является перестановкой с повторениями из 7 элементов. Их число по формуле (1.15):

P₇(3; 2; 2) = 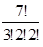= 210.

Решение задач на непосредственное вычисление вероятностей

с использованием формул комбинаторики

Пример 1.15 В урне пять шаров с номерами 1, 2 3, 4, 5. Какова вероятность того, что вынимая наудачу один за другим три шара (без возвращения) получим шары с нечетными номерами в порядке возрастания (1, 3, 5)?

Решение Общее число возможных исходов испытания n - число групп, которые можно образовать из пяти шаров (элементов) по три, различающиеся либо элементами, например, 1, 2, 3 и 1, 2, 4 и т.д., либо порядком их: 1, 2, 3 и 2, 1, 3 и т.д. Это будут размещения из пяти элементов по три Таким образом, n= 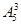= 5Ÿ4Ÿ3 = 60

Событие А - появление трех шаров с нечетными номерами в порядке их возрастания (1, 3, 5)

Благоприятствующим будет лишь один исход - извлечены шары с номерами 1, 3, 5 в порядке их выхода m = 1.

Искомая вероятность равна Р(А) = =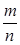

Пример 1.16 Буквы а, а, к, к, о, х, в написаны на отдельных карточках. Какова вероятность того, что извлекая эти карточки по одной наудачу, мы получим в порядке их выхода слово «Каховка».

Решение Всего возможных исходов испытания будет столько сколько можно сделать перестановок из семи элементов (букв, входящих в слово «Каховка») n=P₇ = 1Ÿ2Ÿ3Ÿ4Ÿ5Ÿ6Ÿ7 = 5040

Событие А -такое расположение карточек с названными буквами при котором составлено было бы (в порядке их вы хода) слова «Каховка»

Благоприятными будут те исходы, при которых мы получим слово «Каховка». Число их m установим из следующих соображений: если бы в этом слове не было повторяющихся букв, то благоприятный исход был бы один. Однако в слове «Каховка» буквы «к» и «а» встречаются дважды, и если мы эти буквы поменяем местам, то снова получим то же слово. Следовательно, благоприятных исходов, будет четыре m = 4. Таким образом, Р(А)= 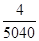=0,000794.

Пример 1.17В ящике 15 .изделий, среди которых три бракованных. Сборщик наудачу берет, два изделия. Какова вероятность того, что оба они окажутся годными?

Решение. Общее число n возможных исходов - это группы элементов (изделий) из 15 по 2, отличающихся по крайней мере одним элементом .(сочетания) n = 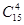. Событие А - оба вынутые изделия годные. Число исходов, благоприятствующих появлению события А - число сочетаний из 12 по 2 (так как годных изделий в ящике 12) m = .

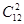Искомая вероятность равна Р(A)= 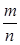= = 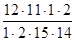=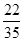0,629.

Замечание. Во многих задачах для непосредственного подсчета вероятности события А в случае безвозвратной .выборки применяется формула

Р(А)= (*)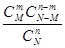

где N - число элементов в партии;

М - число элементов в партии, обладающих некоторым признаком (шары определенного цвета, бракованные изделия и др.);

п - число элементов, выбранных из партии;

т - число элементов, попавших в выборку, обладающих указанным выше признаком.

Событие А - появление m элементов, обладающих указанным признаком, среди n отобранных из партии.

Пример 1.18В научно-исследовательской лаборатории работают 10 сотрудников, из. них 3 женщины. По табельным номерам наудачу выбрали 7 человек. Какова вероятность того, что среди отобранных лиц окажутся 2 женщины?

Решение, В условии нашего примера: N = 10, M = 3, n = 7, т = 2. Событие A - среди отобранных лиц будет 2 женщины. По формуле (*) имеем Р(А)= 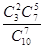=0,525.

ЗАДАНИЕ

1. Пятитомное собрание сочинений расположено на полке в случайном порядке. Какова вероятность того, что книги стоят слева направо в порядке нумерации томов (от 1 до5)?

2. Наудачу взятый телефонный номер состоит из 5 цифр. Какова вероятность того, что в нем все цифры: а) различны; б) одинаковые; в) нечетные? Известно, что номер телефона не начинается с цифры ноль.

3. Из 30 студентов10 имеют спортивные разряды. Какова вероятность того, что выбранные наудачу 3 студента – разрядники?

4. В лифт на 1-м этаже девятиэтажного дома вошли 4 человека, каждый из которых может выйти независимо друг от друга на любом этаже с 2-го по 9-й. Какова вероятность того, что все пассажиры выйдут: а) на 6-м этаже; б) на одном этаже?

⇐ Предыдущая 123 Следующая ⇒