Определение вероятности

1.2. Определение вероятности

Некоторые события наступают достаточно часто, а некоторые — чрезвычайно редко. Введем числовую характеристику, характеризующую этот показатель события.

Определение. Вероятность Р данного события А называется отношение числа исходов т, благоприятствующих появлению данного события, к общему числу п равновозможных, несовместных и образующих полную группу результатов испытаний, т.е.

P(A) = 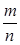(1.1)

Приведенное определение называется классическим и отличается простотой и конструктивностью.

Из определения (1.1) следуют свойства вероятности: для достоверных событий Р=1 (т=п), для невозможных Р=0 (n=0), для случайных 0<Р<1(0<m<n).

Пример 1.3. В группе из 25 студентов пять девушек. Найти вероятность того, что из этой группы первой в аудиторию войдет девушка (джентльменство не учитывается).

Имеем

Р(A)=5/25=0,2.

Пример 1.4. Найти вероятность того, что при бросании игральной кости выпадет грань с четным числом очков.

Имеем

п=6, m=3; Р(A)=3/6=0,5.

Классическое определение имеет, к сожалению, ряд существенных недостатков, а именно: не всегда можно представить результат испытаний как совокупность равновозможных исходов; т и п в (1.1) конечны, но это не всегда так; равновозможностъ и равновероятность — синонимы (в классическом определении содержится порочный круг).

Геометрическое определение вероятности явилось, благодаря попытке отказаться от конечности m и n. Оно состоит в том, что

Р(A)= 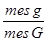(1.2)

где mesg и mesG - меры (длины, площади, объема) пространств всех (G) и благоприятных (g) исходов.

Пример 1.5Два студента договорились встретиться в определенном месте между 15 и 16 часами. Первый, кто придет, ждет второго не более 20 минут и уходит. Какова вероятность их встречи?

Обозначим х - время прихода первого, а у - второго студента. В силу условия задачи должны выполняться двойные неравенства: 3£x£4, 3£y£4.

Введем в рассмотрение прямоугольную систему координат xOy. В этой системе двойным неравенствам удовлетворяют координаты любой точки, принадлежащей квадрату см. 1.2. Таким образом, этот квадрат можно рассматривать как фигуру G.

Встреча произойдет, если разность между моментами прихода студентов меньше 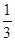, т.е. если y-x< 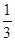при y>x и x-y< 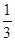при x>y, или, что то же,

y<x + 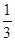при y>x (*)

x< y + 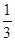при x>y (**)

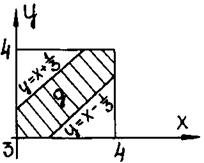
Рис 1.2

Неравенство (*) выполняется для координат тех точек фигуры G, которые лежат выше прямой y=x и ниже прямой y=x + 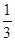; неравенство (**) имеет место для точек, расположенных ниже прямой y=x и выше прямой y=x + .

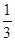Как видно из рис. 1.2, все точки, координаты которых удовлетворяют неравенствам (*) и (**), принадлежат заштрихованному шестиугольнику. Таким образом, этот шестиугольник можно рассматривать как фигуру g, координаты точек которой являются благоприятствующими встрече студентов.

Искомая вероятность

Р(A) = = = = .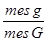

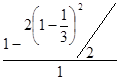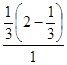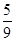Основным понятием статистической .вероятности является относительная частота появления события в результате проведенных испытаний

W(A) = m/n. (1.3)

Здесь п — число проведенных испытаний, a m — число испытаний, в которых событие А появилось.

Отличием относительной частоты от вероятности является то, что первая величина — эмпирическая, определяемая за счет испытаний, а вторая теоретическая, вычисленная до (или без) испытаний.

Определение величины W(A) для различных событий показало, что в одних случаях она для разных серий испытаний меняется мало, а в других — значительно. Если W(A)»C, то событие А называют статистически устойчивым, в противном случае — статистически неустойчивым. В дальнейшем последний случай рассматриваться не будет (как правило, он связан с «человеческим фактором»). Наибольшее количество ошибок, связанных с применением ТВ объясняется попытками анализировать неопределенные (статистические неустойчивые) события, получаемые в испытаниях с большим числом неконтролируемых условий (о какой вероятности выигрыша любимой команды может идти речь, если тренеры заранее договорились «на ничью»). Поэтому в определении случайной величины необходимо предусматривать ее статистическую устойчивость.

Определение. Статистической вероятностью события А называется число, вокруг которого группируются относительные частоты этого события.

Р.Мизес установил, что для случайных событий

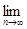Р(A) = W_n(A)

(для неопределенных событий такой предел не существует).

В 1900 г. происходил Второй всемирный математический конгресс, на котором Д.Гильберт выдвинул 23 важнейшие проблемы, адресованные математикам XX в. Шестая проблема Гильберта - построение логически непротиворечивых основ ТВ. Эту проблему решил в 1933 г. А.Н.Колмогоров, предложивший такую систему аксиом, дающую определение вероятности:

1. каждому случайному событию А отвечает неотрицательное число Р(А), называемое вероятностью этого события;

2. для достоверного события Р(А)=1;

3. вероятность появления хотя бы одного из попарно несовместных событий равно сумме вероятностей этих событий.

Методические указания к решению задач

на непосредственное вычисление вероятностей

Анализируя содержание задачи, необходимо установить общее число n возможных исходов испытания; убедиться, что эти исходы несовместны, единственно возможны и равновозможны; определить, вероятность какого именно события надо найти; определить m - число исходов, благоприятствующих появлению интересующего нас события. По формуле (1) подсчитать искомую вероятность.

Пример 1.6Монета подбрасывается три раза. Определить вероятность следующих событий:

а) герб выпадет два раза;

б) герб выпадет хотя бы два раза?

Решение.При трехкратном подбрасывании монеты возможны следующие исходы:

1. Г Г Г 4. Р Г Г 7. Р Г Р

2. Г Г Р 5. Р Р Г 8. Г Р Г,

3. Г Р Р 6. Р Р Р

где Г - выпадение герба,

Р - выпадение решетки.

Число всех возможных .исходов в испытании равно 8. Исходы эти несовместны, единственно возможны и равновозможны.

Событие A - герб выпадет два раза. Ему будут благоприятствовать .исходы 2, 4, 8, т.е. те из восьми, в которых буква Г записана дважды. Таким образом m=3 и Р(A)=3/8.

Событие В - герб выпадет хотя бы два раза при трех бросаниях монеты - означает выпадение герба два или три раза. Благоприятствующими исходами будут 1, 2, 4, 8, т.е. те, в которых буква Г встречается два или три раза, таким образом, m=4. Искомая вероятность равна Р(В) =4/8=0,5.

Пример 1.7Набирая номер телефона, абонент забыл одну цифру и набрал ее наудачу. Какова вероятность того, что набрана нужная цифра?

Решение Абонент мог набрать любую из десяти цифр (0, 1, 2,..., 9). Всего исходов n = 10. Исходы эти несовместны (если набрана какая-то цифра, то никакая другая набранной быть не может), единственно возможны (может быть набрана только одна из этих десяти цифр) и равновозможны (так как одинаково возможно набрать любую из десяти цифр). Событие A - набрана нужная цифра. Благоприятствует событию А лишь один исход (нужная цифра лишь одна) m=1. Следовательно, Р (А) = 1/10 = 0,1.

ЗАДАНИЕ

1. В урне 5 белых и 6 черных шаров. Из урны вынимают наугад один шар. Найти вероятность того, что этот шар – белый.

2. В урне 5 белых и 6 черных шаров. Из урны вынимают один шар и откладывают в сторону. Этот шар оказался белым. После этого из урны берут еще один шар. Найти вероятность того, что этот шар тоже будет белый.

3. В урне 5 белых и 6 черных шаров. Из урны вынимают один шар и, не глядя, откладывают в сторону. После этого из урны берут еще один шар. Этот шар оказался белым. Найти вероятность того, что первый шар, отложенный в сторону, - тоже будет белый.

4. Из урны, в котором 5 белых и 6 черных шаров, вынимают один за другим все шары, кроме одного. Найти вероятность того, что последний оставшийся в урне шар будет белым.

5. Какова вероятность того, что наудачу брошенная в круг точка окажется внутри вписанного в него квадрата?

12 3 Следующая ⇒