Задача Д3

Задача Д3

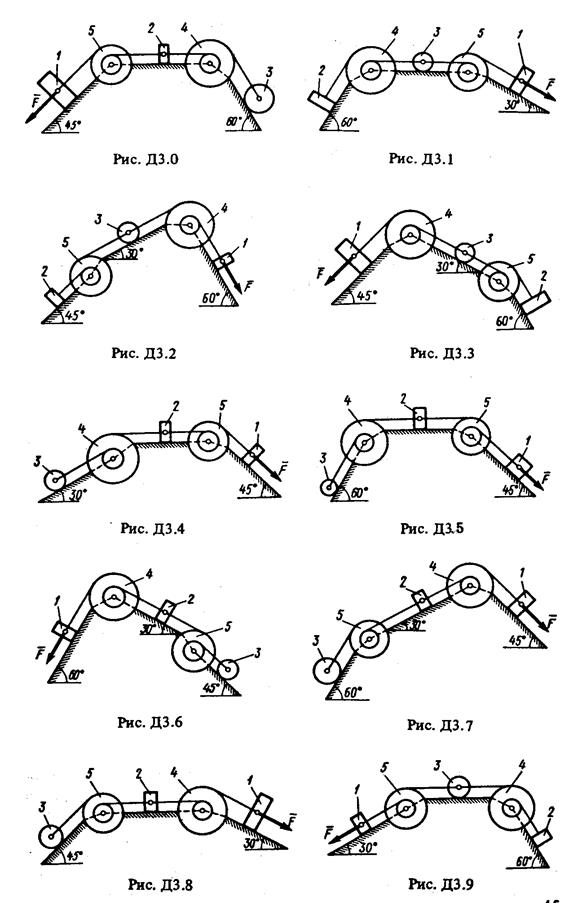
Механическая система состоит из грузов 1 и 2 (коэффициент трения грузов о плоскость f = 0,1), цилиндрического сплошного однородного катка 3 и ступенчатых шкивов 4 и 5 с радиусами ступеней R₄ = 0,3 м, г₄ = 0,1 м, R_s = 0,2 м, r_s = 0,1 м (массу каждого шкива считать равномерно распределенной по его внешнему ободу) (рис. ДЗ.О-Д3.9, табл. ДЗ). Тела системы соединены друг с другом нитями, намотанными на шкивы; участки нитей параллельны соответствующим плоскостям

Таблица ДЗ

Номер условия	m₁ кг	m₂ кг	m₃ кг	m₄ кг	m₅ кг	M₄ Н*м	M₅ Н*м	F = f(f), Н	S₁ м	Найти
							0,8	50(2+ 3s)	1,0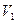
						0,6		20(5 + 2s)	1,2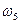
							0,4	80(3 + 4s)	0,8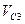
						0,3		40(4 + 5i)	0,6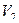
							0,6	30(3 + 2s)	1,4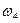
						0,9		40(3 + 5s)	1,6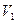
							0,8	60(2 + 5s)	1,0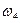
						0,6		30(8 + 3s)	0,8
						0,3		40(2 + 5s)	1,6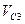
							0,4	50(3 + 2s)	1,4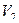

Под действием силы F = f (s) , зависящей от перемещении точки приложения силы, система приходит в движение из состояния покоя. При движении системы на шкивы 4 и 5 действуют постоянные моменты сил сопротивлений, равные соответственно M₄ и M_s,

Определить значение искомой величины в тот момент времени, когда перемещение точки приложения силы 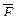равно s₁. Искомая величина указана в столбце "Найти" таблицы, где обозначено: V₁ - скорость груза 1, V_C₃- скорость центра масс катка 3, ω₄ - угловая скорость тела 4 и т.д.

Указания. Задача ДЗ - на применение теоремы об изменении кинетической энергии системы. При решении задачи учесть, что кинетическая энергия системы равна сумме кинетических энергий всех входящих в систему тел: эту энергию нужно выразить через ту скорость (линейную или угловую), которую в задаче надо определить. П0440и вычислении кинетической энергии катка, движущегося плоскопараллельно, для установления зависимости между его угловой скоростью и скоростью его центра масс воспользоваться понятием о мгновенном центре скоростей (кинематика). При определении работы все перемещения следует выразить через заданное перемещение s₁, учтя, что зависимость между перемещениями здесь будет такой же, как между соответствующими скоростями.

Когда по данным таблицы m₂ = 0, груз 2 на чертеже не изображать; шкивы 4 и 5 всегда входят в систему.

Пример ДЗ. Механическая система (рис, ДЗ) состоит из сплошного цилиндрического катка /, ступенчатого шкива 2 с радиусами ступеней R₂ и r₂ (масса шкива равномерно распределена по его внешнему ободу) и груза 3 (коэффициент трения груза о плоскость равен f). Тела системы соединены друг с другом нитями, намотанными на шкив 2.

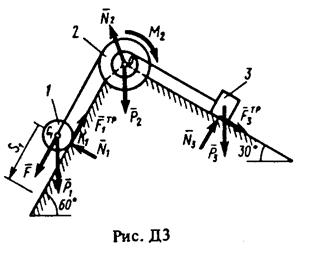
Под действием силы F = зависящей от перемещения s точки ее приложения, система приходит в движения из состояния покоя. При движении на шкив 2 действует постоянный момент М₂сил сопротивления.

Дано: m₁ = 4 кг, m₂ = 10кг, m₃ = 8 кг. R₂ = 0,2 м, r₂ = 0,1 м, f = 0,2, М₂ = 0,6 Н • м, F = = 2(1 + 2s) Н, s_l = 2м,

Определить: скорость V_C₁ центра масс катка, когда s = s₁

Решение. 1. Рассмотрим движение неизменяемой механической системы, состоящей из теп 1, 2. 3, соединенных нитями. Изобразим все действующие на систему внешние силы: активные 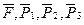, момент сопротивления М₂, реакции 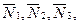и силы трения 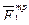и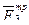

Для определения V_C₁ воспользуемся теоремой об изменении кинетической энергии системы

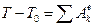. (1)

2. Определяем Т₀ и Т. Так как в начальный момент система находилась в покое, то Т₀ = 0. Величина T равна сумме энергий всех тел системы:

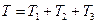(2)

Учитывая, что тело 1 движется плоскопараллельно, тело 3 - поступательно, а тело 2 вращается вокруг неподвижной оси, получим

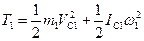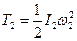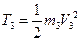, , (3)

Все входящие сюда скорости следует выразить через искомую V_C₁. Приняв во внимание, что точка K₁ - мгновенный центр скоростей катка 1, и обозначив радиус катка через г₁, получим

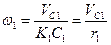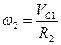
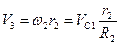, . (4)

Кроме того, входящие в (3) моменты инерции имеют значения

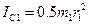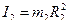, (5)

Подставив все величины (4) и (5) в равенство (3), а затем используя равенство (2), получим окончательно:

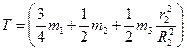
3. Теперь найдем сумму работ всех действующих внешних сил при том перемещении, которое будет иметь система, когда точка С₁ пройдет путь s . Одновременно все перемещения следует выразить через заданную величину s₁ , для чего учтем, что здесь зависимость между перемещениями будет такой же. как и между соответствующими скоростями в равенствах (4). т.е. 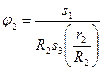В результате получим:

, ,

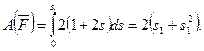
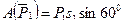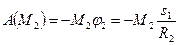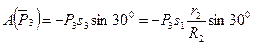
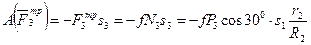
Работа остальных сил равна нулю, так как точка К₁, где приложены , и 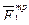- мгновенный центр скоростей, точка О. где приложены 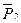и 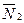. неподвижна, а реакция 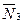, перпендикулярна перемещению груза 3. Тогда окончательно

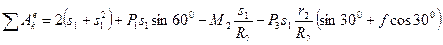(7)

4. Подставив выражения (6) и (7) в уравнение (I) и учитывая, что T₀ = 0, получим

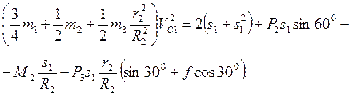(8)

При числовых значениях, которые имеют заданные величины, равенство (8) дает 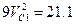. Отсюда находим искомую скорость. Ответ; 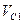= 1,53 м/с.

⇐ Предыдущая 1 2 3 4 5 6 78