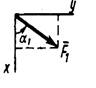Задача С2

Задача С2

Однородная прямоугольная плита весом Р = 5 кН со сторонами АВ = 3l, ВС = 2l закреплена в точке А сферическим шарниром, а в точке В цилиндрическим шарниром (подшипником) и удерживается в равновесии невесомым стержнем СС' (рис. С2.О-С2.9) .

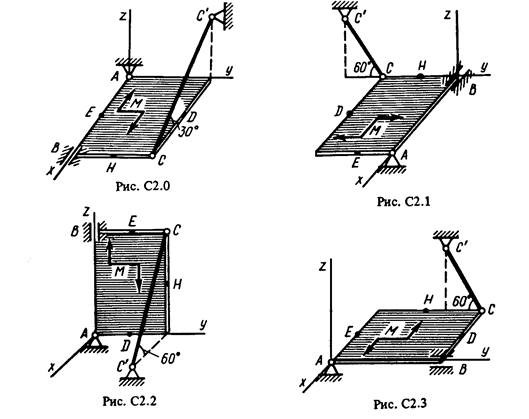
Таблица С2

Сила
Номер условия	F₁= 4 кН		F₂ = 6 кН		F₃ = 8 кН		F₄= 10 кН
	Точка прилож.		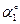Точка прилож.		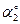Точка прклож.		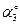Точка прклож.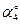
	D H - - E - - E - -	- - - - - -	- D E - - D H H - E	- - - -	E - - E H H - - D D	- - - -	- - D H - - D - E -	- - - - - -

На плиту действуют пара сил с моментом М= 6 кН·м, лежащая в плоскости плиты, и две силы. Значения этих сил, их направления и точки приложения указаны в табл. С2; при этом силы F₁ и F₄ лежат в плоскостях, параллельных плоскости ху, сила F₂ — в плоскости, параллельной xz, сила F₃ — в плоскости, параллельной yz. Точки приложения сил (D, Е, Н) находятся в серединах сторон плиты.

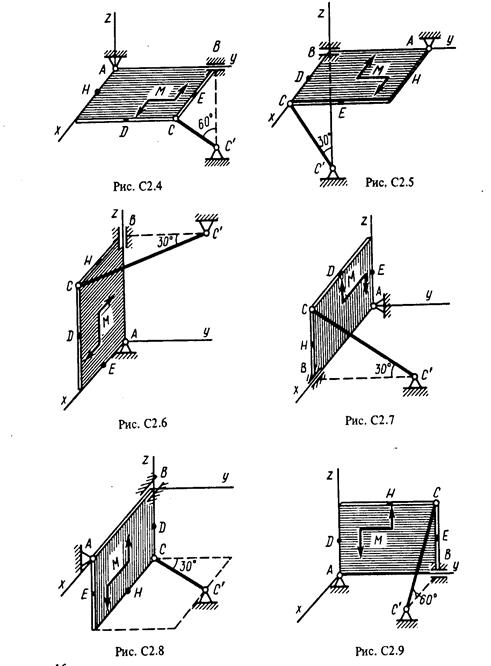
Определить реакции связей в точках А, В и С. При подсчетах принять l = 0,8м.

Указания. Задача С2 — на равновесие тела под действием пространственной системы сил. При ее решении учесть, что реакция сферического шарнира (или подпятника) имеет три составляющие, а реакция цилиндрического шарнира (подшипника) — две составляющие, лежащие в плоскости, перпендикулярной оси шарнира. При вычислении моментов силы F тоже часто удобно разложить ее на составляющие F' и F", параллельные координатным осям; тогда, по теореме Вариньона. m_x (F) = m_x (F' )+ + m_x (F") и т.д.

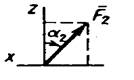
Пример С2. Вертикальная прямоугольная плита весом Р (рис. С2) закреплена сферическим шарниром в точке А, цилиндрическим (подшипником) в точке В и невесомым стержнем DD', лежащим в плоскости, параллельной плоскости yz. На плиту действуют сила F₁, (в плоскости xz), сила F₂, (параллельная оси у) и пара сил с моментом М (в плоскости плиты).

Дано: Р= 5 кН, М= 3 кН • м, F₁ = 6 кН, F₂ = 7,5 кН, α = 30⁰, АВ = 1 м, ВС = 2 м, СЕ = 0,5 АВ, BК = 0,5 ВС.

0пределить: реакции опор А, В и стержня DD'.

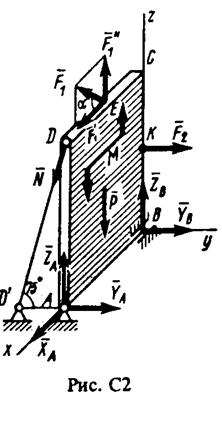Решение. 1. Рассмотрим равновесие плиты. На нее действуют заданные силы Р, F₁, F₂, и пара сил с моментом М, а также реакции связей. Реакцию сферического шарнира разложим на три составляющие Х_A, У_A, Z_A, цилиндрического (подшипника) — на две составляющие Y_B, Z_B (в плоскости, перпендикулярной оси подшипника), реакцию N стержня на- правим вдоль стержня, предполагая, что он растянут.

2. Для определения шести неизвестных реакций составляем шесть уравнений равновесия действующей на плиту пространственной системы сил:

Σ F_kx = 0, Х_A + F₁, соs α = 0, (1)

Σ F_ky = 0, Y_A + Y_B+ F₂ — N cos 75⁰ = 0, (2)

Σ F_kz = 0, Z_A + Z_B — Р — N sin 75⁰ + F₁ sin α = 0, (3)

Σ m_x (F_k) = 0, — F₂* ВК + N cos 75⁰* BC = 0, (4)

Σ m_y (F_k) = 0, Р * AB/2 + F₁ cos α * BC — F₁ sin α * AB/2—Z_A* AB + N sin 75⁰ * AB+ M = 0, (5)

Σ m_z(F_k) = 0, Y_A * АВ — N cos 75⁰ * АВ= 0. (6)

Для определения момента силы F₁, относительно оси у разлагаем F₁, на составляющие F'₁, и F"₁, параллельные осям х и z (F'₁ = F₁* соs α, F"₁ = F₁* sin α), и применяем теорему Вариньона (см. указания). Аналогично можно поступить при определении моментов реакции N.

Подставив в составленные уравнения числовые значения всех задан- ных величин и решив затем эти уравнения, найдем, чему равны искомые реакции.

0 т в е т: Х_A = -5,2 кН, Y_A = 3,8 кН, Z_A = 28,4 кН, Y_B = — 7,5 кН, Z_B = —12,4 кН, N = 14,5 кН. Знаки указывают, что силы Х_A, Y_B и Z_B направлены противоположно показанным на рис. С2.

⇐ Предыдущая 123 4 5 6 7 8 Следующая ⇒