Лекция 21. Предел функции в точке. Основные теоремы о пределах.

Лекция 21. Предел функции в точке. Основные теоремы о пределах.

1. Понятие предела функции в точке

Предел — одно из основных понятий математического анализа. Различают предел последовательности и предел функции.

Мы будем рассматривать только предел функции в точке.

Пусть дана функция y = f(x), точка x = a. Пусть значение функции в этой точке существует и равно b, тогда говорят, что существует предел функции при x → a и этот предел равен b

В записи определение будет выглядеть следующим образом: 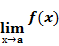= 𝑏

Видим, что запись предела состоит из трех частей:

1) значка предела lim (сокращение латинского слова limes — предел и равнозначного французского limite). Но, использовать при чтении предела слово лимит— не принято.

2) записи под значком предела, в данном случае x → a. Запись читается «икс стремится к a». Чаще всего – именно x, хотя вместо «икса» на практике встречаются и другие переменные. На месте a может находиться совершенно любое число, а также бесконечность ( + ∞ «плюс бесконечность» либо – ∞ «минус бесконечность»);

3) функции под знаком предела, в данном случае f(x).

Пример 1. Прочитать запись lim _𝑥_→1(𝑥²+4𝑥−12𝑥+4)

Решение. Предел функции 𝑓(𝑥)=𝑥²+4𝑥−12𝑥+4 при «икс» стремящемся к 1.

Теперь разберем следующий важный вопрос — а что значит выражение «икс стремится к единице»? И что вообще такое «стремится»?

Понятие предела — это понятие, если так можно сказать, динамическое.

Построим последовательность: сначала x = 1,1; затем x = 1,01; x = 1,001; x = …; x = 1,00000001; …. То есть выражение «икс стремится к единице» следует понимать так — «икс» принимает значения, которые бесконечно близко приближаются к единице и практически с ней совпадают.

12 3 4 Следующая ⇒