Найти: tg φ.. Решите самостоятельно.

⇐ ПредыдущаяСтр 3 из 3

Найти: tg φ.

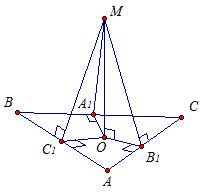
4. ОТ – проекция наклонной МТ на плоскость ABC.

Значит, ∠(МТ, АВС) = ∠(МТ, ОТ) = ∠МТО.

Аналогично, ∠(МТ₁, АВС) = ∠(МТ₁, ОТ₁) = ∠МТ₁О.

Мы доказали, что треугольники МОТ и МОТ₁равны, а значит, и углы МТО и МТ₁О равны. Обозначим, их величину за φ.

Тогда, ∠(МТ, АВС) = ∠(МТ₁, АВС) = φ, что и требовалось доказать.

5. Рассмотри прямоугольный треугольник МОТ.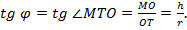

Ответ: .

Д/З:

Решите самостоятельно.

1. Точка А отстоит от плоскости на расстоянии 12 см. Найдите длины наклонных, проведенных из этой точки, если они образуют с плоскостью углы: а) 30°; б) 45°; в) 60°.

2. Длина наклонной АК, проведенной из точки А к плоскости α равна 8 см, а угол между прямой и этой плоскостью равен 60°. Найдите длину проекции наклонной на плоскость α.

3. Найти расстояние от точки К до плоскости равностороннего треугольника со стороной 6 см и равноудаленной от его вершин на расстояние равное 8см.

4. Прямая ОК перпендикулярна к плоскости ромба ABCD, диагонали которого пересекаются в точке О.

а) Докажите, что расстояние от точки К до всех прямых, содержащих стороны ромба, равны.

б) Найдите это расстояние, если ОК = 4,5 дм, АС = 8 дм, BD = 6 дм.

⇐ Предыдущая 1 23