Перпендикуляр и наклонные. Угол между прямой и плоскостью»

Практическая работа по геометрии №2

«Перпендикуляр и наклонные. Угол между прямой и плоскостью»

Теория:

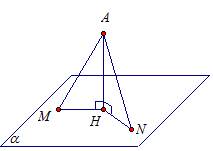
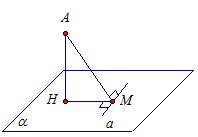
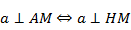
Рассмотрим плоскость α.

Точка А лежит вне плоскости α. Отрезок АН перпендикулярен плоскости α.

Отрезок АН – перпендикуляр, проведенный из точки А к плоскости α

. Точка Н – основание перпендикуляра.

Отрезок АМ – наклонная, М – основание наклонной.

Отрезок МН называется проекцией наклонной АМ на плоскость α

Свойство 1. Длина перпендикуляра меньше, чем длина наклонной. То есть, АН < AM.

Расстоянием от точки А до плоскости α называют длину перпендикуляра АН.

Обозначение: ρ(А; α) = АН.

Точка Н – проекция точки А на плоскость α.

Свойство 2.

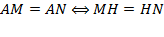
То есть, если из точки А проведены равные наклонные, АМ = AN,

то их проекции равны: MH = HN.

Если проекции равны MH = HN, то равны и наклонные: АМ = AN.

Задача

Прямая ОМ перпендикулярна плоскости треугольника АВС и проходит через центр О вписанной в него окружности.

Докажите, что точка М равноудалена:

1. от прямых АВ, ВС, СА.

2. от всех точек вписанной окружности и от всех касательных к ней.

3. Найдите это расстояние, если известны радиус r окружности и длина ОМ = h.

4. Докажите равенство углов наклона прямых МТ (где Т – любая точка окружности) к плоскости АВС.

5. Найдите тангенс этих углов.