Доказать: ∠(МТ, АВС) = ∠(МТ1, АВС) = φ.

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

пункт 1.

Дано: ∆АВС,

О – центр вписанной окружности,

ОМ ⊥ АВС.

Доказать: ρ (М, АВ) = ρ (М, ВС) = ρ (М, СА)

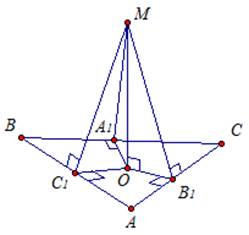Доказательство:

Пусть А₁, В₁, С₁ – это точки касания окружности к сторонам треугольника.

ОС₁, ОА₁, ОВ₁ – радиусы этой окружности.

Тогда, по свойству, ОС₁ ⊥ АВ, ОА₁ ⊥ ВС, ОВ₁ ⊥ АС.

МО – перпендикуляр к плоскости АВС.

ОС₁ – проекция наклонной МС₁ на плоскость АВС.

Так как ОС₁ ⊥ АВ, то МС₁ ⊥ АВ (по теореме о трех перпендикулярах).

Значит, МС₁ – это расстояние от точи М до прямой АВ, МС₁ = ρ (М, АВ).

Аналогично получаем, что МА₁ = ρ (М, ВС), МВ₁ = ρ (М, СА).

Треугольники МОС₁, МОА₁, МОВ₁ равны по двум катетам (катеты ОС₁, ОА₁, ОВ₁равны как радиусы вписанной окружности, катет ОМ – общий).

Из равенства треугольников следует, что МС₁ = МА₁ = МВ₁.

А значит, ρ (М, АВ) = ρ (М, ВС) = ρ (М, СА), что и требовалось доказать.

пункт 2

Прямая ОМ перпендикулярна плоскости треугольника АВС и проходит через центр О вписанной в него окружности.

Докажите, что точка М равноудалена от всех точек вписанной окружности и от всех касательных к ней.

Дано: ∆АВС,

О – центр вписанной окружности,

ОМ ⊥ АВС.

Доказать: ρ (М, Т) = ρ (М, Т₁)

ρ (М, t) = ρ (М, t₁)

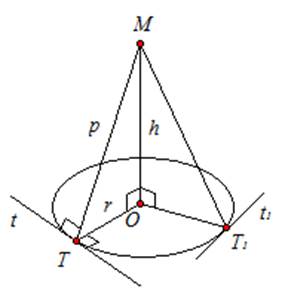Рассмотрим вспомогательную иллюстрацию и введем некоторые дополнительные обозначения.

Имеем окружность с центром в точке О и радиусом r, ОМ ⊥ ОТ₁Т, ОМ = h, OT = r

Пусть t₁, t – две произвольные касательные. Т₁, Т – точки касания касательных t₁, t к окружности

Доказательство:

Касательные t₁, t касаются окружности в точках Т, Т₁ соответственно.

Радиус, проведенный в точку касания касательной, перпендикулярен касательной.

То есть ОТ ⊥ t.

ρ (М, Т) = МТ, ρ (М, Т₁) = МТ₁

ОТ – это проекция наклонной МТ на плоскость окружности.

Прямая t лежит в этой плоскости.

Так как ОТ ⊥ t, то МТ ⊥ tпо теореме о трех перпендикулярах)

. Значит, ρ (М, t) = МТ.

Аналогично, ρ (М, t₁) = МТ₁.

Рассмотрим прямоугольные треугольники МОТ и МОТ₁.

Катет ОМ – общий, ОТ = ОТ₁как радиусы.

Значит, треугольники МОТ и МОТ₁ равны по двум катетам.

Следовательно, МТ = МТ₁, а значит

ρ (М, t) = ρ (М, t₁), ρ (М, Т) = ρ (М, Т₁),

что и требовалось доказать.

пункт 3

Дано: ∆АВС,

О – центр вписанной окружности,

ОМ ⊥ АВС

Найти: ρ (М, t)

Решение:

Рассмотри прямоугольный треугольник МОТ

Из теоремы Пифагора:

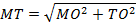
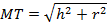
Ответ: .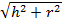

пункт 4,5

Дано: ∆АВС,

О – центр вписанной окружности,

ОМ ⊥ АВС

Доказать: ∠(МТ, АВС) = ∠(МТ1, АВС) = φ.

⇐ Предыдущая 123 Следующая ⇒