Сопряжение.

2. Сопряжение.

Сопряжением называется плавный переход от одной линии к другой. Дуги окружностей, при помощи которых выполняется сопряжение, называются дугами сопряжения. Для построения дуги сопряжения необходимо на чертеже определить ее центр, радиус этой дуги и точки сопряжения, в которых дуга сопряжения переходит в сопрягаемые линии.

Задаваясь радиусом сопряжения остальные параметры можно определить графически. На рис. 4 показано построение сопряжения пересекающихся прямых линий при помощи дуги. Параметр R является радиусом сопряжения. Точки T₀ и T₁ полученные на пересекающихся прямых AB и BC являются точками сопряжения. Точка О – центр сопряжения.

На рис. 4а, из точки пересечения прямых В проводится дуга окружности радиусом равным радиусу сопряжения R до пересечения с прямыми в точках Т₁ и Т₀ - точки сопряжения. Из полученных точек тем же радиусом провести дуги окружностей до взаимного их пересечения в точке О. Из точки О радиусом сопряжения R провести дугу сопряжения.

Для построения сопряжения двух пересекающихся прямых под острым углом (рис. 4б) заданного радиуса R необходимо на расстоянии R провести прямые , параллельные заданным до пересечения в точке D. Основания перпендикуляров, опущенных из точки D на прямые АВ и ВС будут точками сопряжения – Т₁ и Т₀. Дуга радиуса R проведённая из точки О и будет дугой сопряжения.

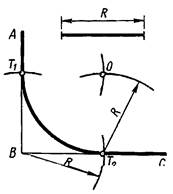
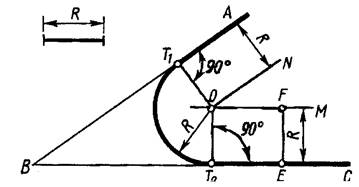
а) б)

Рисунок 4 - Сопряжение пересекающихся прямых линий при помощи дуги: а) составляющих прямой угол; б) пересекающихся под углом отличным от прямого

На рис. 5 показано построение сопряжения дуги окружности и прямой а с помощью дуги заданного радиуса. Для определения центра сопряжения О на расстоянии равном заданному радиусу сопряжения R параллельно прямой а проводят прямую m а из центра О₁ радиусом (R + R₁) дугу концентрической окружности. На пересечении проведённой дуги и прямой m определяется точка О – центр дуги сопряжения. Точка сопряжения К₁ определяется на пересечении прямой О₁О и окружности, точка сопряжения К центры О₁ и О соединяют и на определяют точку, точка определяется, как основание перпендикуляра проведённого из точки О к прямой а. Радиусом сопряжения R из точки О проводится дуга сопряжения.

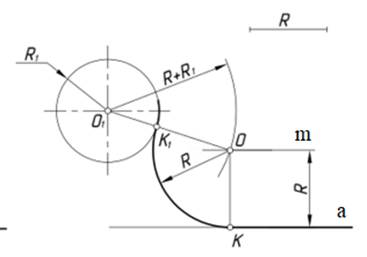
Рисунок 5 – Сопряжение дуги окружности и прямой линии

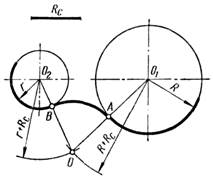
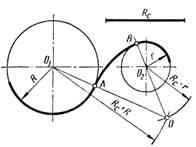
Построение сопряжения двух дуг окружностей дугой заданного радиуса может быть внешним, внутренним и смешанным. При внешнем сопряжении сопрягаемые дуги находятся с внешней стороны сопряжения. Пример построения такого вида сопряжения показан на рис. 6а. Из центра О₁ радиусом (R + R_c) и из центра О₂ радиусом (r + R_c) проводят дуги до пересечения в точке О. Точки сопряжения А и В лежат на линиях, соединяющих точку О с центрами дуг О₁ и О₂. Из точки О как из центра проводят дугу сопряжения радиусом R_c.

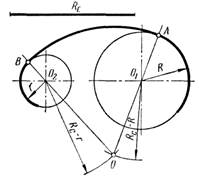
Внутреннее сопряжение дуг окружностей при помощи третьей характеризуется тем, что сопрягаемые дуги находятся внутри дуги сопряжения (рис. 6б). Из центра О₁ проводится дуга радиусом (R_c- R), а из центра О₂ - дуга радиусом (R_c - r). В пересечении этих дуг получаем точку О – центр дуги сопряжения. Точки сопряжения А и В лежат на прямых, соединяющих точку О с центрами заданных окружностей О₁ и О₂. Из точки О как из центра проводят дугу сопряжения радиусом R_c.

Смешанное сопряжение двух данных дуг окружностей третьей дугой характеризуется тем, что одна сопрягаемая дуга находится внутри дуги сопряжения, а другая – вне ее (рис. 6в). Из центра О₁ проводится дуга радиусом (R_c+ R), а из центра О₂ – радиусом (R_c - r). Пересечение проведённых дуг определяет центр дуги сопряжения точку О. Точки сопряжения А и В лежат на прямых, соединяющих точку О с центрами заданных окружностей О₁ и О₂. Из точки О как из центра проводят дугу сопряжения радиусом R_c.

а) б)

в)

Рисунок 6 – Сопряжение двух дуг третьей дугой: а) внешнее; б) внутреннее;

в) смешанное

⇐ Предыдущая 1 23