Эвольвента

Эвольвента

Эвольвента описывается точкой прямой линии, катящейся без скольжения по неподвижной кривой линии.

Исходную окружность с центром О разделить на произвольное число равных частей. В точках деления 1, 2…12 провести касательные к окружности, направленные в одну сторону. Последовательно отмечаем на всех касательных точки соответствующие определённому числу делений длины окружности: на первой – одному делению, на второй – двум, на третьей – трём и т.д. Соединяем полученные точки плавной кривой линией (рис. 2).

Нормаль n эвольвенты в точке X представляет собой касательную к окружности. Касательная t в точке X перпендикулярна к нормали n.

Рисунок 2 – Построение эвольвенты

Винтовая линия

Винтовая линия относится к пространственным кривым. Различают цилиндрические, конические, сферические и другие винтовые линии.

Цилиндрическая винтовая линия рассматривается как траектория движения точки, равномерно вращающейся вокруг оси и одновременно равномерно перемещающейся в направлении этой оси.

Построение проекций цилиндрической винтовой линии и её развёртки показано на рис. 3. Исходными данными служат: D – диаметр цилиндра, h – шаг винтовой линии и ее направление - в данном случае правое. Шаг винтовой линии h – равен полному обороту винтовой линии вокруг цилиндра.

Для построения проекций винтовой линии фронтальную и горизонтальную проекции цилиндра делим на 12 равных частей. Фронтальная проекция каждой последующей точки, например А2₂ смещена относительно предыдущей точки А1₂ вдоль оси цилиндра на 1/12 часть шага h и находится на линии связи с соответствующей горизонтальной проекцией – точкой А2₁.

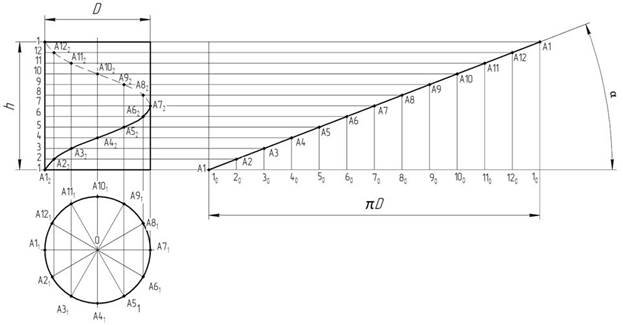
Рисунок 3 – Построение винтовой линии

Фронтальная проекция винтовой линии представляет собой деформированную синусоиду.

При развёртке цилиндрической поверхности на плоскость, винтовая линия представляет собой прямую. Угол α – угол подъёма винтовой линии. Винтовая линия пересекает все образующие цилиндра, на поверхности которого она расположена, под одним и тем же углом.

⇐ Предыдущая 123 Следующая ⇒