Лекция № 4.. Кривые линии. Сопряжение.. Кривые линии.. Эллипс

Лекция № 4.

Кривые линии. Сопряжение.

Цель лекции: познакомиться с алгоритмом построения плоских и пространственных кривых на примере некоторых линий и с образованием линейчатых поверхностей.

1. Кривые линии.

Эллипс

Эллипсом называется геометрическое место точек плоскости, сумма расстояний от каждой из которых до двух данных точек F1 и F2 (фокусов) этой плоскости есть величина постоянная.

Построение эллипса по двум осям осуществляется по точкам. Рассмотри поэтапное черчение:

1.) строятся окружности с разными диаметрами;

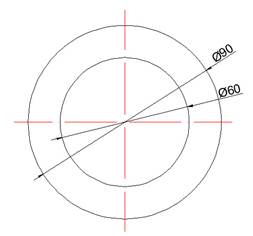
2.) окружности делятся на 12 частей;

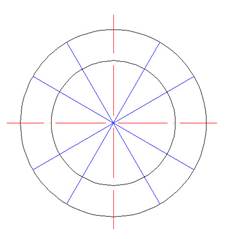
Деление окружности на 12 частей показано на видео.

3.) проводятся вспомогательные вертикальные линии (сиреневый цвет) от краев большего диаметра;

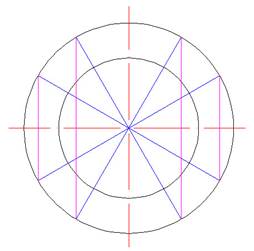
4.) чертятся горизонтальные вспомогательные линии (зеленый цвет) от края окружности меньшего диаметра до вертикальных линий;

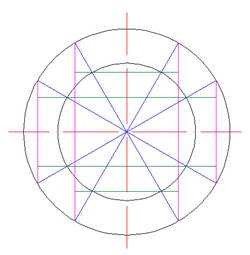
5.) в пересечении вспомогательных линий обозначаются точки;

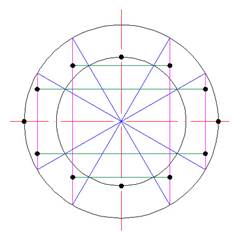
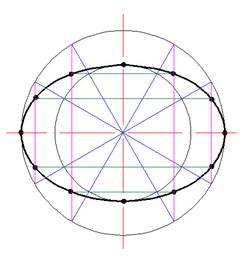
6.) точки между собой соединяются плавной линией.

Для нахождения фокусов F1 и F2 надо из точки С, как из центра, провести дугу радиусом R = OA, она пересечет ось АВ в точках F1 и F2. Для построения касательной и нормали (биссектриссы) в произвольной точке К эллипса, соединяем точку К с фокусами F1 и F2. Делим образованный угол F1KF2 пополам, т.е. строим бисектрису данного угла. Биссектриса является нормалью эллипса в точке К. Перпендикулярно нормали проводим касательную к эллипсу в точке К (рис. 1).

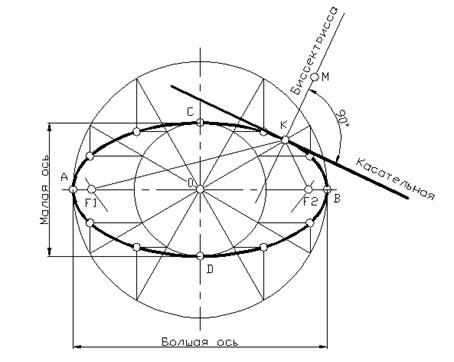
Рисунок 1 – Построение эллипса по 2-м осям

Нормаль к кривой в заданной её точке — прямая, перпендикулярная к касательной прямой в указанной точке кривой.

Касательная прямая — прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка.

12 3 Следующая ⇒