
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Прямая и плоскость в пространстве
2.3. Прямая и плоскость в пространстве
Угол между прямой и плоскостью. За угол между прямой и плоскостью принимается угол, образованный этой прямой и ее проекцией на рассматриваемую плоскость.
| l |
| Q |
Здесь определяются два угла – острый и тупой. Выбирается один из них.
Пусть плоскость (Q) задана общим уравнением Ax + By + Cz + D = 0, а прямая (l) задана каноническими уравнениями 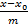 =
= 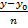 =
= 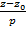 . Синус угла
. Синус угла 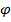 между прямой (l) и плоскостью (Q) вычисляется по формуле
между прямой (l) и плоскостью (Q) вычисляется по формуле
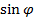 =
= 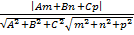 .
.
Условие параллельности прямой и плоскости:
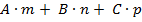 = 0.
= 0.
Условие ортогональности прямой и плоскости:
 =
=  =
=  .
.
Равенства вида
являются условием принадлежности прямой плоскости. Первое равенство отражает тот факт, что прямая параллельна плоскости, а второе – что плоскость проходит через точку на прямой.
Замечание. Уравнения прямой на плоскости получаются путем исключения входящих в пространственные уравнения компонент, относящихся к переменной z. Например из канонического уравнения прямой в пространстве получаются уравнения прямой на плоскости вида 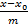 =
= 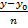 .
.
Пример. Стороны AB и BC параллелограмма заданы уравнениями 2x – y + 5 = 0 и x – 2y + 4 = 0. Диагонали его пересекаются в точке M(1; 4). Найти уравнения двух других сторон параллелограмма.
Решение. Изобразим параллелограмм на чертеже.
| B |
| C |
| M |
| A |
| D |
Находим координаты точки пересечения прямых AB и BC, решая систему уравнений:
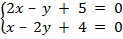
Это будет точка B(-2; 1). Теперь найдем координаты точки D, которые обозначим как 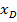 и
и 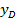 . Так как точка M находится на середине отрезка BD, то должны выполняться равенства:
. Так как точка M находится на середине отрезка BD, то должны выполняться равенства:
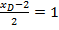 ,
, 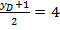 .
.
Отсюда находим 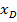 = 4,
= 4, 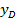 =7 и D(4; 7).
=7 и D(4; 7).
Угловые коэффициенты прямых AB и CD совпадают и равны 2. Уравнение прямой CD находим из условия, что ее угловой коэффициент равен 2 и она проходит через точку D(4;7):
y – 7 = 2(x – 4), или 2x – y -1 = 0.
Аналогично находим уравнение прямой AD:
x – 2y +10 = 0.
2.4. Контрольные вопросы
1. Какие Вы знаете уравнения плоскости?
2. Какой смысл имеют коэффициенты A, B, C в уравнении плоскости Ax + By + Cz + D = 0?
3. Плоскость проходит через ось Oz. Какие из коэффициентов A, B, C, D в этом случае равны 0?
4. Какой смысл имеют коэффициенты a, b, c в уравнении плоскости  +
+  +
+  = 1?
= 1?
5. Укажите нормирующий множитель для перехода от общего уравнения плоскости к нормальному.
6. Какие Вы знаете уравнения прямой в пространстве?
7. Какой смысл имеют коэффициенты m, n. p в уравнении прямой 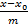 =
= 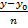 =
= 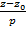 ?
?
8. Определяет ли прямую система
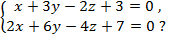
2.5. Расчетное задание
Даны координаты четырех точек в пространстве A1, A2, A3, A4 (см. табл.1). Требуется решить следующие задачи:
1) составить уравнение плоскости Q, проходящей через точки A1, A2, A3;
2) составить канонические уравнения прямой, проходящей через точку A4 перпендикулярно плоскости Q;
3) найти координаты точки пересечения такой прямой с плоскостью Q;
4) найти расстояние от точки A4 до плоскости Q;
5) составить уравнение плоскости, проходящей через точку A4 параллельно плоскости Q;
6) составить уравнение плоскости, проходящей через точки A1 и A4 перпендикулярно плоскости Q;
7) найти косинус угла между плоскостью Q и плоскостью, проходящей через точки A1, A3, A4;
8) найти синус угла между прямой A1A4 и плоскостью Q.
2.5. Решение типовых задач
Задача 1. Составить уравнение плоскости, проходящей через точки A1(3; -1; 2), A2(4; -1; -1), A3(2; 0; 2).
Решение. Воспользуемся уравнением плоскости, проходящей через три заданные точки:
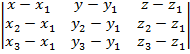 =
= 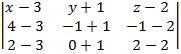 =
= 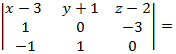 0.
0.
Раскрываем определитель третьего порядка:
3(x – 3) + 3(y + 1) + z – 2 = 0, или 3x + 3y + z – 8 = 0.
Задача 2. Составить канонические уравнения прямой, проходящей через точку A(-1; 2; 1) перпендикулярно плоскости 3x – 2y + z – 12 = 0.
Решение. В качестве направляющего вектора искомой прямой можно взять нормальный вектор заданной плоскости, то есть считаем 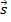 = {3; -2; 1}. Тогда канонические уравнения прямой записываются в виде
= {3; -2; 1}. Тогда канонические уравнения прямой записываются в виде
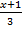 =
= 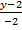 =
= 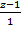 .
.
Задача 3. Найти точку пересечения прямой 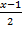 =
= 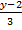 =
= 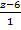 и плоскости 2x – 6y – z + 1 = 0.
и плоскости 2x – 6y – z + 1 = 0.
Решение. Запишем уравнения заданной прямой в параметрическом виде:
x = 1 + 2t ; y = 2+ 3t ; z = 6 + t .
Пусть значение параметра t = ta соответствует точке A(xa; ya; za) пересечения прямой и плоскости. Тогда значение ta находится из уравнения:
2(1 + 2ta) – 6(2+ 3ta) – (6 + ta) +1 = 0.
Решая его, получим ta = -1.
Координаты точки пересечения A(xa; ya; za) находим из параметрических уравнений прямой при t = -1:
xa = 1 + 2(-1) = -1; ya = 2+ 3(-1) = -1; za = 6 - 1 = 5.
Значит, точка A(-1; -1; 5) есть точка пересечения прямой и плоскости.
Задача 4. Найти расстояние от точки A(-2; -4; 3) до плоскости 2x – y +2z + 3 = 0.
Решение. Воспользуемся формулой d = 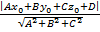 =
= 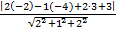 = 3.
= 3.
Задача 5. Составить уравнение плоскости, проходящей через точку A(2; -1; 6) параллельно плоскости x + y - 2z + 5 = 0.
Решение. В качестве нормального вектора искомой плоскости можно взять нормальный вектор заданной плоскости 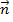 = {1; 1; -2}. Искомая плоскость представляется уравнением
= {1; 1; -2}. Искомая плоскость представляется уравнением
1(x – 2) + 1(y + 1) – 2(z – 6) = 0, или x + y - 2z + 11 = 0.
Задача 6. Составить уравнение плоскости, проходящей через точки A1(1; 2; 3) и A2(2; 1; 1) перпендикулярно плоскости 3x + 4y + z - 6 = 0.
Решение. Пусть точка M(x; y; z) принадлежит искомой плоскости. Тогда векторы 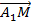 ,
, 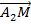 и нормальный вектор заданной плоскости
и нормальный вектор заданной плоскости 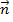 = {3; 4; 1} должны быть комплонарны. Значит выполняется условие
= {3; 4; 1} должны быть комплонарны. Значит выполняется условие
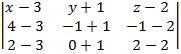 = 0.
= 0.
Раскрывая определитель третьего порядка, получим искомое уравнение плоскости
x - y + z - 2 = 0.
Задача 7. Найти косинус угла между плоскостями x - y 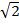 + z - 1 = 0 и x + y
+ z - 1 = 0 и x + y 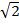 - z + 3 = 0.
- z + 3 = 0.
Решение. Воспользуемся формулой
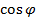 =
= 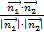 =
= 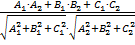 =
= 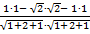 = -
= -  .
.
Задача 8. Найти синус угла между прямой 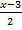 =
= 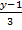 =
= 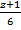 и плоскостью 6x + 15y - 10z + 31 = 0.
и плоскостью 6x + 15y - 10z + 31 = 0.
Решение. Воспользуемся формулой
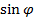 =
= 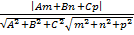 =
= 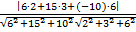 =
= 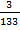 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|