
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Плоскость и прямая в пространстве
1. Плоскость и прямая в пространстве
1.1. Уравнения плоскости
Уравнение плоскости, проходящей через данную точку и имеющей данный нормальный вектор. Пусть в пространстве задана точка M0(x0; y0; z0) и вектор 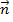 = {A; B; C}. Плоскость, проходящая через точку M0(x0; y0; z0) и перпендикулярная к ненулевому вектору
= {A; B; C}. Плоскость, проходящая через точку M0(x0; y0; z0) и перпендикулярная к ненулевому вектору 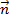 (нормальному вектору) представляется следующим уравнением:
(нормальному вектору) представляется следующим уравнением:
A(x - x0) + B(y - y0) + C(z - z0) = 0.
Это уравнение отражает тот факт, что вектор 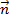 ортогонален любому вектору
ортогонален любому вектору 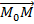 на плоскости. Точка M(x; y; z) – произвольная точка плоскости.
на плоскости. Точка M(x; y; z) – произвольная точка плоскости.
| z |
| y |
| x |
| O |
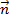
|
| M |
| M0 |
Общее уравнение плоскости имеет следующий вид:
Ax + By + Cz + D = 0.
Уравнение плоскости, проходящей через три заданные точки. Пусть в пространстве заданы три точки M1(x1; y1; z1), M2(x2; y2; z2), M3(x3; y3; z3) не лежащие на одной прямой. Проходящая через них плоскость представляется уравнением
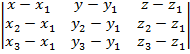 = 0.
= 0.
Это уравнение отражает компланарность векторов 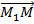 ,
, 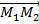 ,
, 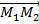 . Точка M(x; y; z) – произвольная точка плоскости.
. Точка M(x; y; z) – произвольная точка плоскости.
| M |
| M1 |
| M2 |
| M3 |
Уравнение плоскости в отрезках. Пусть плоскость проходит через три точки A(a; 0; 0), B(0; b; 0), C(0; 0; c), отсекая на координатных осях не равные нулю отрезки a, b, c. Тогда ее уравнение имеет вид
 +
+  +
+  = 1.
= 1.
| c |
| b |
| a |
| z |
| y |
| x |
Нормальное уравнение плоскости:
x  + y
+ y 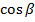 + z
+ z 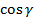 - p = 0,
- p = 0,
где  ,
, 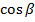 ,
, 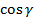 - направляющие косинусы нормального вектора плоскости
- направляющие косинусы нормального вектора плоскости 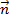 ;
;
p – расстояние от начала координат до плоскости. Считается, что вектор 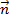 направлен от начала координат к плоскости (начало вектора
направлен от начала координат к плоскости (начало вектора 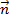 связывают с началом координатной системы и смотрят его направление – к плоскости или от плоскости). Это уравнение отражает тот факт, что проекция вектора, проведенного из начала О в произвольную точку плоскости, всегда равна значению p.
связывают с началом координатной системы и смотрят его направление – к плоскости или от плоскости). Это уравнение отражает тот факт, что проекция вектора, проведенного из начала О в произвольную точку плоскости, всегда равна значению p.
Общее уравнение плоскости Ax + By + Cz + D = 0 приводится к нормальному виду умножением на нормирующий множитель 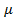 =
= 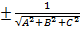 . Знак нормирующего множителя берется противоположным знаку свободного члена D в общем уравнении плоскости.
. Знак нормирующего множителя берется противоположным знаку свободного члена D в общем уравнении плоскости.
Пример. Составить общее уравнение плоскости, проходящей через точку P(-1; 2; 2), параллельно векторам 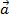 = {2; -2; 3} и
= {2; -2; 3} и 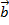 = {4; 1; 5}.
= {4; 1; 5}.
Решение.Вначале находим нормальный вектор 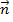 искомой плоскости по формуле
искомой плоскости по формуле
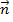 =
= 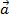
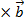 =
= 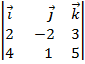 =
= 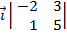 -
- 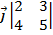 +
+ 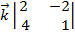 = - 13
= - 13 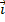 + 2
+ 2 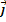 + 10
+ 10 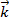 .
.
Получили, что 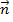 = {-13; 2; 10}.
= {-13; 2; 10}.
Теперь составим уравнение плоскости, которая проходит через заданную точку P и перпендикулярна вектору 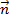 :
:
-13(x + 1) + 2(y – 2) + 10(z – 2) = 0.
Отсюда находим общее уравнение искомой плоскости: -13x + 2y + 10z – 37 = 0.
Угол между плоскостями. Под углом между плоскостямипонимается один из двугранных углов, образованный этими плоскостями (либо острый, либо тупой).
| Q1 |
| Q2 |
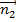
|
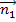
|
Пусть плоскости заданы своими общими уравнениями
(Q1): A1x + B1y + C1z + D1 = 0 ;
(Q2): A2x + B2y + C2z + D2 = 0.
За угол 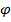 между плоскостями(Q1) и (Q2) принимается угол между нормальными векторами плоскостей
между плоскостями(Q1) и (Q2) принимается угол между нормальными векторами плоскостей 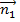 = {A1; B1; C1} и
= {A1; B1; C1} и 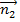 = {A2; B2; C2} и его косинус находится по формуле
= {A2; B2; C2} и его косинус находится по формуле
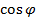 =
= 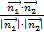 =
= 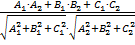 .
.
Условие ортогональности двух плоскостей. Если плоскость (Q1) ортогональна плоскости (Q2), то их нормальные векторы будут также ортогональны, а тогда 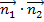 = 0 и
= 0 и
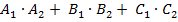 = 0.
= 0.
Условие параллельности двух плоскостей. Если плоскость (Q1) параллельна плоскости (Q2), то их нормальные векторы коллинеарны, а тогда
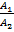 =
= 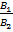 =
= 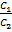 .
.
Расстояние от точки до плоскости. Пусть в пространстве задана точка M0(x0; y0; z0) и плоскость (Q): Ax + By + Cz + D = 0. Расстояние d от точки M0 до плоскости (Q) находится по формуле
d = 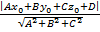 .
.
Формула выводится из условия, что d есть модуль проекции вектора 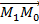 на направление нормального вектора
на направление нормального вектора 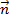 , M1 – произвольная точка плоскости.
, M1 – произвольная точка плоскости.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|