
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Уравнения прямой в пространстве
2.2. Уравнения прямой в пространстве
Канонические уравнения прямой. Пусть в пространстве задана точка M0(x0; y0; z0) и вектор 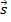 = {m; n; p}. Уравнения прямой (l), которая проходит через точку M0 и которая параллельна вектору
= {m; n; p}. Уравнения прямой (l), которая проходит через точку M0 и которая параллельна вектору 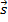 , имеют следующий вид:
, имеют следующий вид:
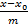 =
= 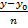 =
= 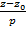 .
.
Эти уравнения называются каноническими и отражают тот факт, что вектор 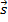 , который называется направляющим вектором прямой, коллинеарен вектору
, который называется направляющим вектором прямой, коллинеарен вектору 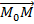 . Точка M(x; y; z) – произвольная точка прямой (l).
. Точка M(x; y; z) – произвольная точка прямой (l).
| M |
| M0 |
| l |
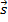
|
Параметрические уравнения прямой. Запишем канонические уравнения прямой в виде
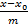 =
= 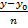 =
= 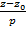 = t, где t – параметр. Решая каждое из трех записанных таким образом уравнений относительно x, y, z, получим параметрические уравнения прямой
= t, где t – параметр. Решая каждое из трех записанных таким образом уравнений относительно x, y, z, получим параметрические уравнения прямой
x = x0 + mt; y = y0 + nt; z = z0 + pt.
Уравнения прямой, проходящей через две заданные точки. Пусть в пространстве заданы две точки M1(x1; y1; z1) и M2(x2; y2; z2). Уравнения прямой, проходящей через эти точки, имеют вид
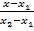 =
= 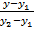 =
= 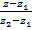 .
.
Эти уравнения получаются из канонических уравнений прямой, если взять за точку на прямой точку M1 а за направляющий вектор - вектор 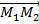 .
.
Общие уравнения прямой:
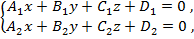
где нормальные векторы плоскостей 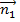 = {A1; B1; C1} и
= {A1; B1; C1} и 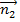 = {A2; B2; C2} не коллинеарны. Здесь прямая определяется как линия пересечения двух непараллельных плоскостей.
= {A2; B2; C2} не коллинеарны. Здесь прямая определяется как линия пересечения двух непараллельных плоскостей.
От общих уравнений прямой можно перейти к каноническим уравнениям следующим образом. Координаты точки на прямой получаются из системы уравнений, задав одной из координат произвольное значение (например z = 0).
Пример. Даны вершины треугольника A(2; -3; 4), B(5; -1; -2), C(4; -2; 5). Составить
параметрические уравнения его медианы CD.
Решение. Изобразим треугольник ABC и его медиану CD на чертеже.
| A |
| C |
| D |
| B |
Находим координаты xD, yD, zD точки D по формулам:
xD = 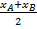 =
= 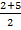 = 3,5; yD =
= 3,5; yD = 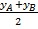 =
= 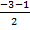 = - 2; zD =
= - 2; zD = 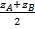 =
= 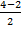 = 1.
= 1.
Вектор 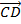 является направляющим вектором медианы CD. Его координаты находим по формуле:
является направляющим вектором медианы CD. Его координаты находим по формуле:
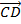 = {xD – xC ; yD – yC ; zD – zC} = {3,5 – 4; -2 +2; 1 – 5} = {-0,5; 0; -4}.
= {xD – xC ; yD – yC ; zD – zC} = {3,5 – 4; -2 +2; 1 – 5} = {-0,5; 0; -4}.
Теперь запишем параметрические уравнения медианы CD как прямой, проходящей через точку C(4; -2; 5) и имеющей направляющий вектор 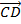 = {-0,5; 0; -4}:
= {-0,5; 0; -4}:
x = 4 + 0,5t ; y = -2 ; z = 5 + 4t .
Расстояние от точки до прямой. Пусть в пространстве задана точка M1(x1; y1; z1) и прямая (l) своими каноническими уравнениями 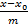 =
= 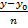 =
= 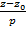 . Расстояние d от точки M1 до прямой (l) находится по формуле
. Расстояние d от точки M1 до прямой (l) находится по формуле
d = 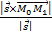 ,
,
где 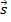 = {m; n; p} – направляющий вектор прямой (l), M0(x0; y0; z0) – точка прямой. Здесь расстояние d находится как высота треугольника, построенного на векторах
= {m; n; p} – направляющий вектор прямой (l), M0(x0; y0; z0) – точка прямой. Здесь расстояние d находится как высота треугольника, построенного на векторах  и
и 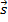 ,
,
Угол между прямыми. Пусть прямые (l1) и (l2) заданы своими каноническими уравнениями
(l1): 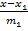 =
= 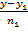 =
= 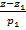 ,
,
(l2): 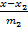 =
= 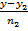 =
= 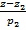 .
.
За угол между прямыми (l1) и (l2) принимается угол 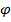 , образованный направляющими векторами прямых
, образованный направляющими векторами прямых 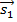 = {m1; n1; p1} и
= {m1; n1; p1} и 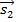 = {m2; n2; p2} и его косинус находится по формуле
= {m2; n2; p2} и его косинус находится по формуле
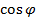 =
= 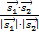 =
= 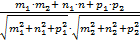 .
.
Условие ортогональности двух прямых:
 = 0.
= 0.
Условие параллельности двух прямых:
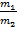 =
= 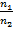 =
= 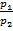 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|