Задача №12. Задача №13

Задача №12

12 задача из демоверсии ЕГЭ по математике базового уровня посвящена теме “экстремум”. Здесь необходимо найти производную функции и ее критические точки.

Пример задачи

Турист подбирает себе экскурсионную программу. Сведения о некоторых музеях и парках, подготовленные туристическим бюро, представлены в таблице.

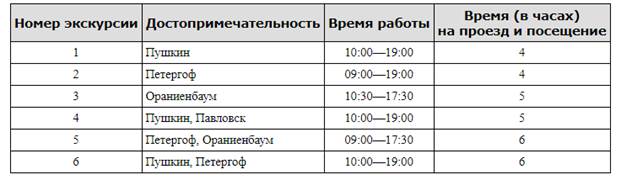
Пользуясь таблицей, подберите экскурсионную программу так, чтобы турист посетил не ме-нее трёх достопримечательностей за один день.

В ответе для подобранной программы укажите номера экскурсий без пробелов, запятых и других дополнительных символов.

Решение

У туриста всего 10 часов. Если он выберет шестую экскурсию, то на третью экскурсию времени уже не хватит, а вот если выберет пятую, то вполне успевает и на первую. Та-ким образом, 5 и 1.

При выборе четвертой успевает только на вторую. Таким образом, 4 и 2. При выборе третьей посмотреть три достопримечательности никак не успеет.

Ответ: 1 и 5 или 2 и 4.

Задача №13

Задания из этого раздела демо-варианта ЕГЭ проверяют знание стереометрии. Необходимо знать формулы нахождения площадей разных фигур: прямоугольного параллелепипеда, призмы, пирамиды, куба, цилиндра и т. д.

Пример задачи

В правильной треугольной пирамиде SABC медианы основания ABC пересекаются в точке O. Площадь треугольника ABC равна 2; объем пирамиды равен 4. Найдите длину отрезка OS.

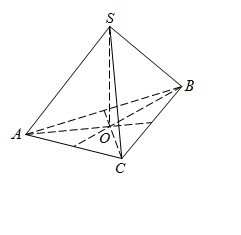
Решение

Отрезок OS высотой треугольной пирамиды SABC, ее объем выражается формулой

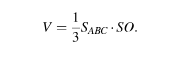
Значит,

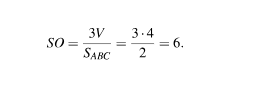
Ответ: 6.

⇐ Предыдущая 1 2 3 456 7 8 9 Следующая ⇒