Задача 5.

Задача 5.

Анализ. Пусть 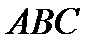— искомый треугольник. Величина 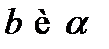являются элементами треугольника 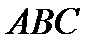. Чтобы

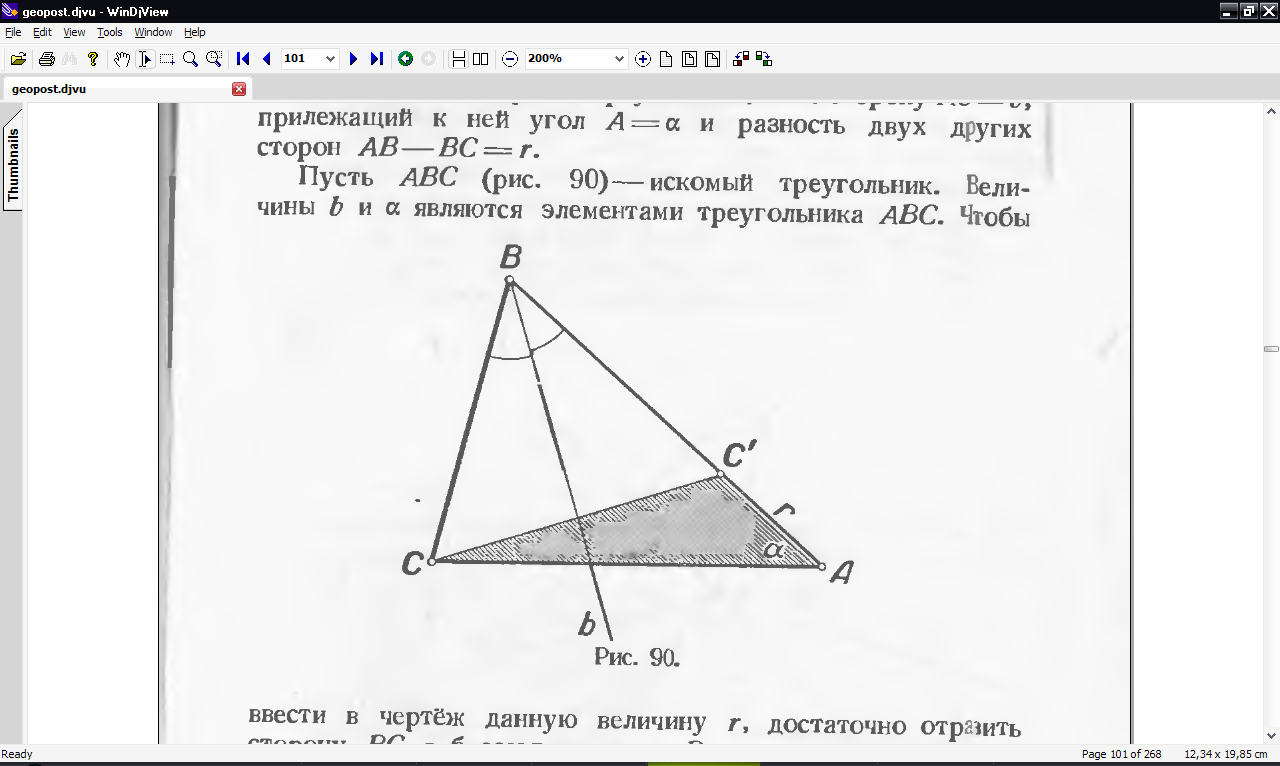
ввести в чертёж данную величину 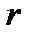, достаточно отразить сторону 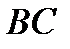в биссектрисе угла 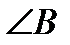; если при этом точка 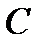преобразуется в точку 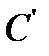, то точка 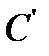окажется на стороне 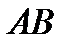, причем отрезок 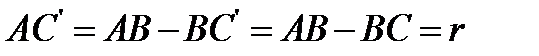. В треугольнике 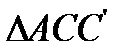теперь известны две стороны и угол между ними, так что он легко может быть построен. Кроме этого, замечаем, что биссектриса угла 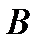перпендикулярна прямой 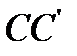и делит отрезок 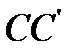пополам.

Построение.

1. построим прямую ;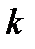

2. на прямой 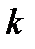отметим отрезок ;

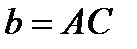3 .построим ;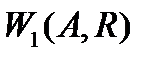

4. 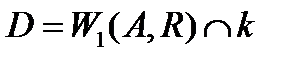и построим 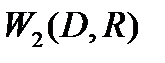, причем радиусы 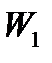и 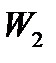равны;

5. ;

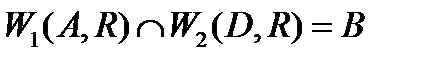6. ;

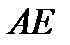7. отметим на прямой 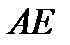отрезок равный ;

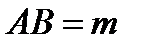8. ;

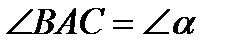9. 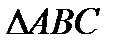- искомый.

Итак, для построения треугольника 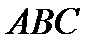надо предварительно построить треугольник 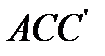по двум сторонам и углу между ними, а затем провести прямую, перпендикулярную 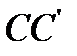, через середину отрезка 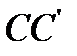до пересечения с лучом 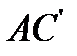; эта точка пересечения и будет третьей вершиной 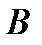искомого треугольника.

Доказательство.

1. ;

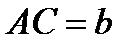2. ;

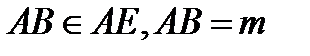3. 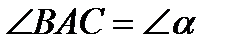- по построению.

Исследование. Заметим прежде всего, что по условию 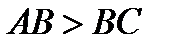и поэтому 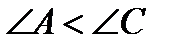, следовательно, угол 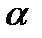должен быть острым. При этом условии симметраль точек 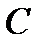и 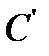пересечёт луч 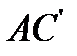в том и только в том случае, когда 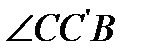острый, т. е. 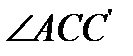тупой, так что отрезок 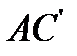меньше проекции отрезка 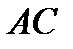на прямую .

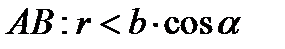Это неравенство не может осуществиться, если 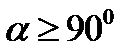. Таким образом, соотношение 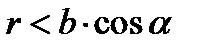выражает условие (однозначной) разрешимости задачи.

Замечание. Если 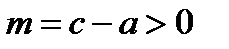, то такой треугольник можно построить; если 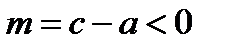, то такой треугольник нельзя построить.

⇐ Предыдущая 1 23