Хелпикс

Главная

Контакты

Случайная статья



Задача 1.. Задача 2.

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒


Задача 1.

A’
F
B
A
l
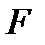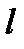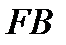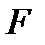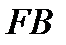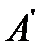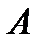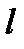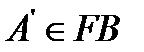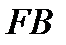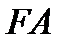Анализ: точка  построена как пересечение  и , но так как  искомая, то для фиксации  найдем другую точку, можно взять точку  симметричную  относительно  (точка , так как  и  симметричны относительно  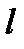по условию).

Построение:

1. строим точку 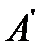 симметричную точке  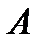относительно ;

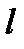A’
F’=F
B
A
l
О
2. ;

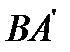3. ;

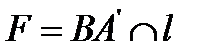4. 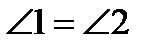, т.е. 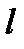- биссектриса .

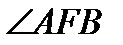                                                             Доказательство.

1. по построению 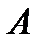 и 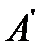симметричны относительно прямой ;

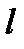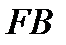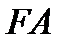2.  и  симметричны относительно ;

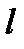3. 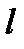 - биссектриса.

Исследование.

A’
B
A
l
О
A’
F
A
l
Бесконечно много решений.                                           Нет решений.

 

 

Задача 2.

Анализ. Пусть 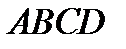 – квадрат, удовлетворяющий условиям, а именно: вершина 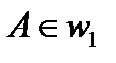, вершина 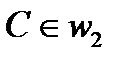, вершины  и  лежат на прямой 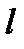 (см. а). Построим окружность 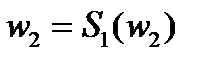. Так как диагональ  квадрата является его осью симметрии, то вершина  квадрата отобразится на вершину 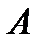. Но вершина 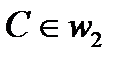, и поэтому вершина .

  

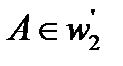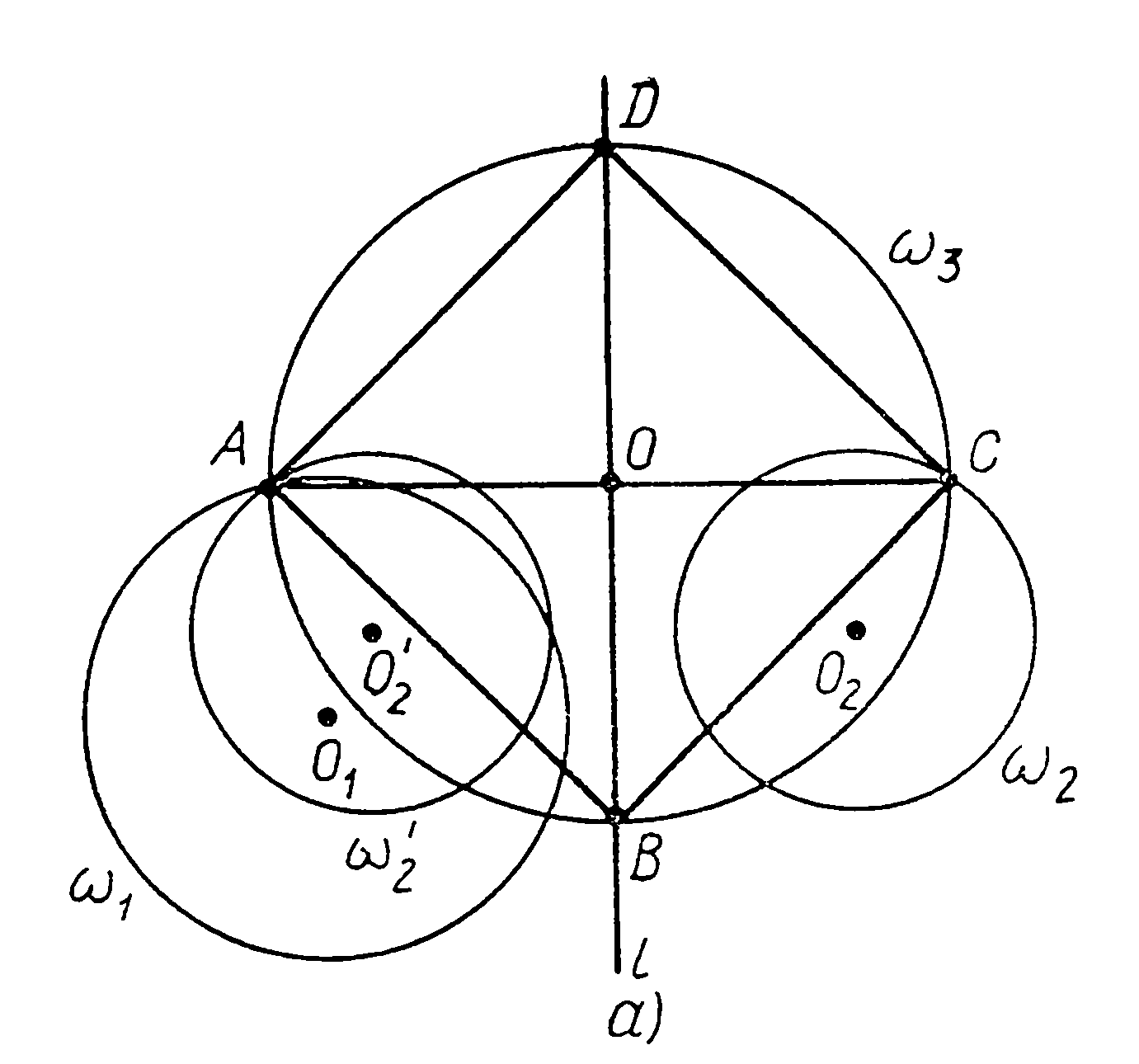
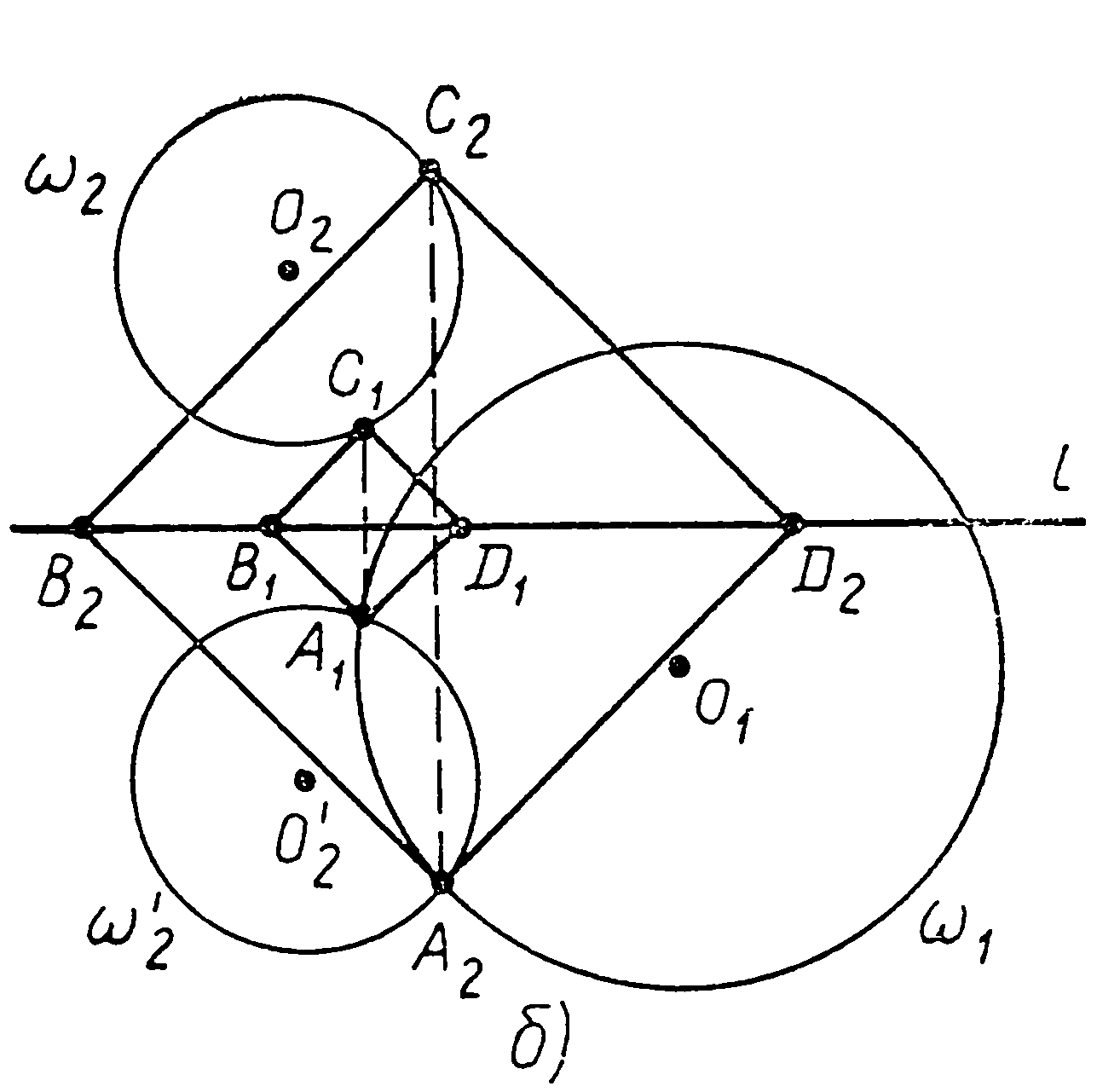
Построение. Строим окружность , находим точку , которую отображаем на точку 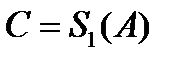. На 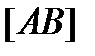 как на диаметре строим окружность  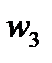  и находим точку  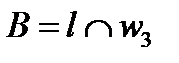и .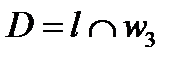

Доказательство. Так как 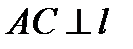, то при симметрии относительно  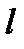прямая  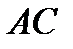отображается на себя. Кроме того, окружность  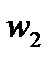 симметрична окружности  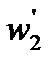. Тогда точка 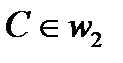. Далее, отрезок  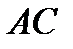– диаметр окружности 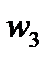, точка  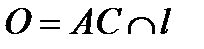– центр окружности 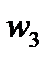, поэтому 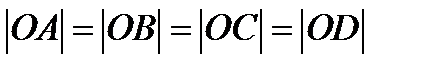. Так как далее 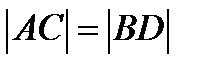, , 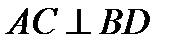то 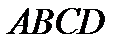 - квадрат. Итак, по построению 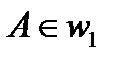, , 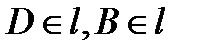а по доказанному  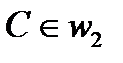и четырёхугольник  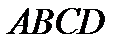- квадрат.

Таким образом, четырёхугольник 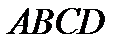 удовлетворяют всем поставленным условиям, т.е. является искомым квадратом.

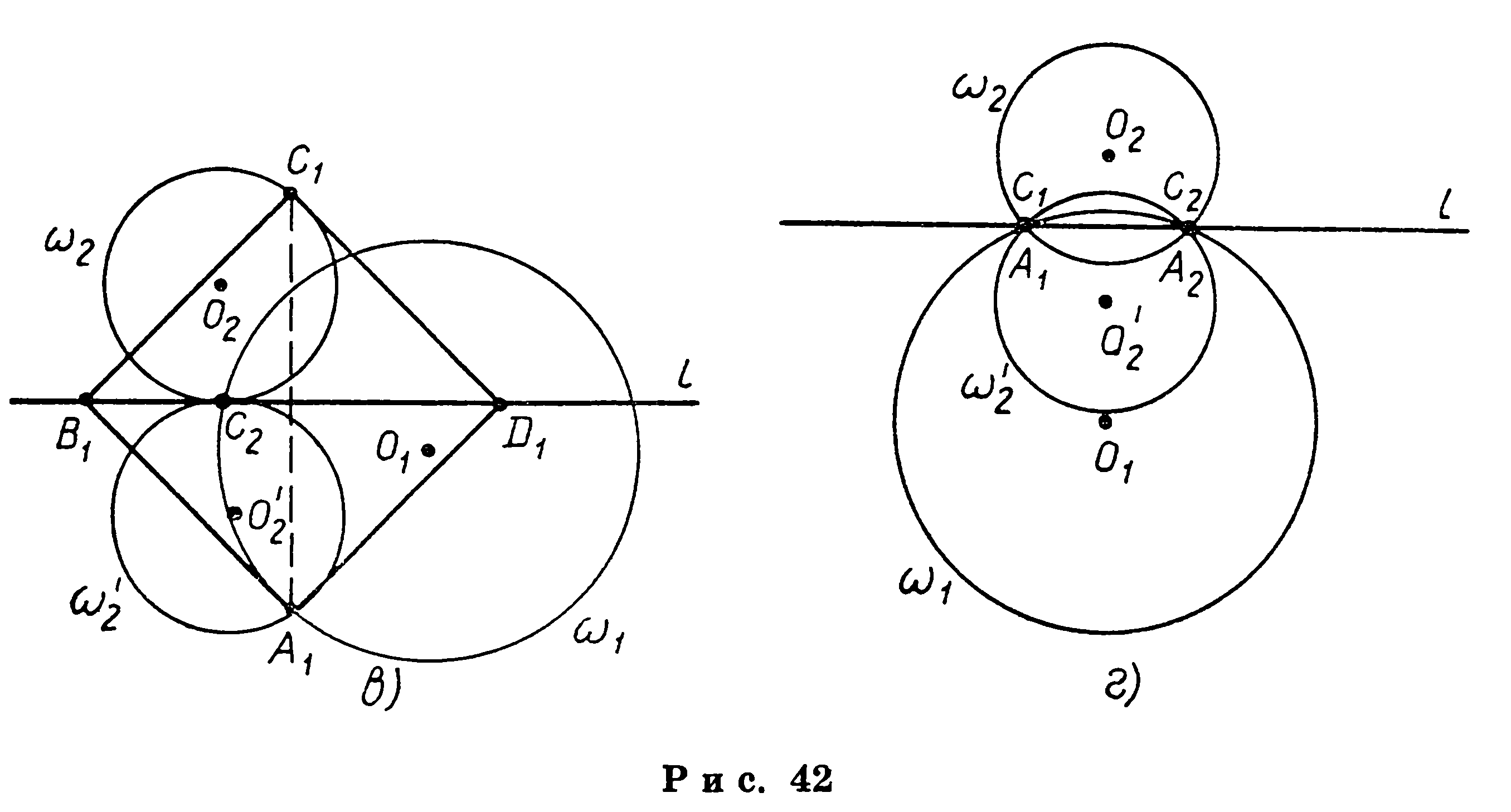
Исследование. При выбранном способе построения количество решений зависит от количества точек пересечения окружностей 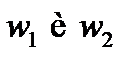, и положения этих точек относительно . Возможны следующие случаи:

1) если окружности 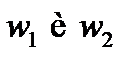 пересекаются, то задача либо имеет два решения (б), либо имеет одно решение (в), либо не имеет решений (г);

2) если окружности 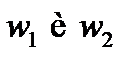 касаются, то либо имеется одно решение, либо решений нет;

3) если окружности 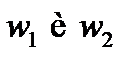 не имеют общих точек, то решений нет;

4) если окружности 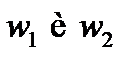 совпадают, то решений бесконечное множество.

 

Задача 3.

Анализ. Пусть 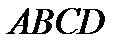 – искомый ромб, .

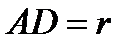Замечаем, что задача о построении ромба сводится к построению одной какой-либо из его вершин, например вершины 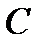. По свойствам ромба точки 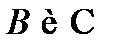симметричны относительно прямой . Поэтому при зеркальном отражении от прямой  точка 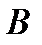 преобразуется в точку 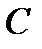, а следовательно, прямая  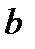– в некоторую прямую 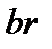, проходящую через точку 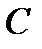. 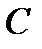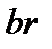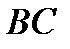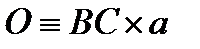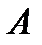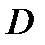Таким образом, точка  может быть построена как точка пересечения прямых  и ; прямую ; точку ; точка  и  на прямой 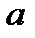, отстоящие от точки  на расстояние .  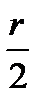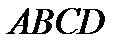– искомый ромб.

Построение.

1. 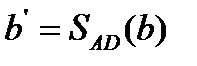 - образ прямой  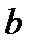относительно ;

2. ;

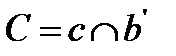3. строим симметричную точке  относительно ;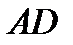

4. ;

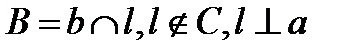5. строим ;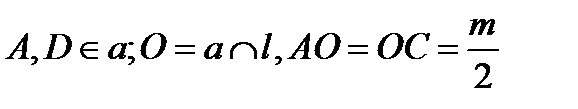

6. - искомый ромб.

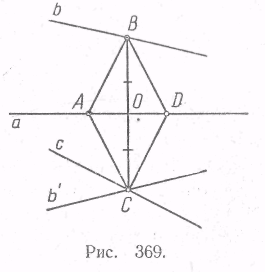
Рис. 5

 

Доказательство.

1. по построению диагонали  точкой пересечения делятся пополам;

2. диагонали  пересекаются под прямым углом;

3. - ромб.

Исследование. Возможны следующие случаи:

1) 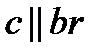 , решений нет;

2) 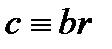, решений бесконечно много;

3) прямые 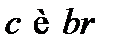 пересекаются вне прямой , одно решение;

4) прямые 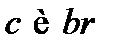 пересекаются на прямой 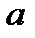, решений нет.

Сущность приёма, применённого в последнем примере, состоит в следующем: задача сводится к построению точки, причём эта точка оказывается общей точкой некоторой данной фигуры и фигуры, симметричной другой данной фигуре относительно некоторой оси.

Аналогичный приём применяется также в задачах, решаемых при помощи других геометрических преобразований.


 

Задача 4.

l
O
B
n
 
A
m
t
l
O
B
n
 
A
m
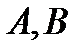Анализ. Из условия следует, что точки  симметричны относительно прямой 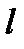. . 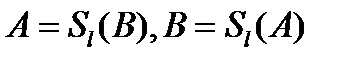Рассмотрим симметрию плоскости относительно  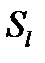и пусть  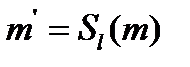симметричная прямой  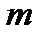относительно прямой. Так как  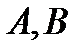симметричны, то прямая  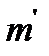пройдет через точку 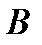. Таким образом точку  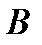построим, как пересечение  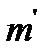и 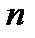, тогда точка 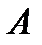построим как точку симметричную точке  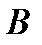относительно прямой .

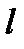X
Построение.

T=T’
1. строим ;

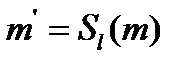2. прямая ;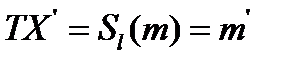

X’
3. ;

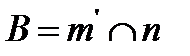4. ;

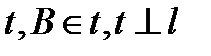m’
5. ;

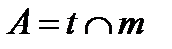6. 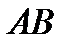 - искомый результат.

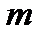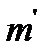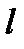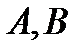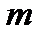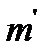Доказательство. По построению  и  - симметричны относительно , точки  лежат на прямых  и  симметричных  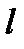и на прямой 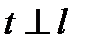. Отсюда следует, что точки  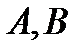симметричны относительно прямой 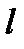. Отсюда . 

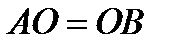Исследование.

1. решение будет есл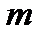и  и 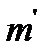 не параллельны;

2. если прямые 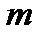 и 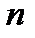 параллельны 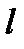, но не симметричны ей, то решений не будет;

3. если прямые 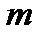 и 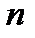 симметричны 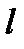, то решений бесконечно много;

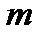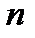4. в общем случае если  и  симметричны 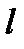, то бесконечно много решений.


 


⇐ Предыдущая123Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.