
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Метод симметрии. Симметрия. Метод симметрии
Метод симметрии
Подготовил студент 502 группы
Математический факультет
Ненартович Марк Витольдович
Минск 2012
Симметрия
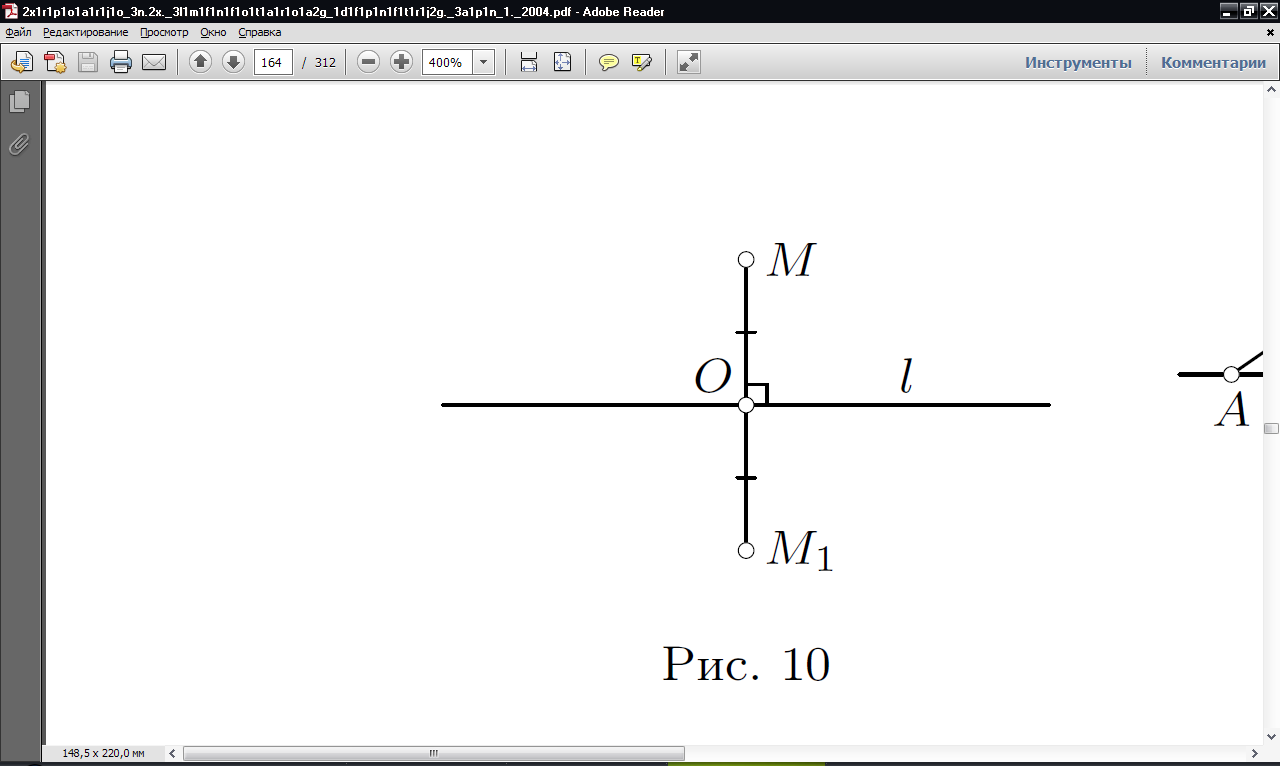
Опр.: Точки 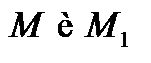 называются симметричными относительно заданной прямой
называются симметричными относительно заданной прямой 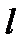 , если эта прямая является серединным перпендикуляром к отрезку
, если эта прямая является серединным перпендикуляром к отрезку 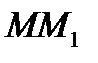 (Рис. 1). Каждая точка прямой
(Рис. 1). Каждая точка прямой 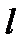 симметрична сама себе. Преобразование плоскости, при котором каждая точка отображается на симметричную ей точку относительно данной прямой
симметрична сама себе. Преобразование плоскости, при котором каждая точка отображается на симметричную ей точку относительно данной прямой 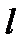 , называется осевой симметрией с осью
, называется осевой симметрией с осью 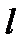 и обозначается
и обозначается 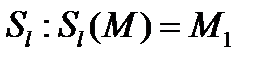 .
.
Фигура 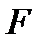 и ее образ
и ее образ 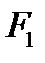 при осевой симметрии называются симметричными фигурами относительно прямой
при осевой симметрии называются симметричными фигурами относительно прямой 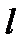 (Рис. 2).
(Рис. 2).

Теорема. Осевая симметрия плоскости есть движение.
Теорема. Прямая, отличная от перпендикуляра к оси симметрии, и ее образ при этой симметрии пересекаются на оси симметрии или ей параллельны.
Прямая 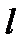 называется осью симметрии фигуры
называется осью симметрии фигуры 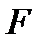 , если при симметрии с осью
, если при симметрии с осью 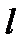 фигура
фигура 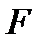 отображается на себя:
отображается на себя: 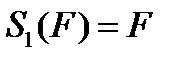 . Говорят, что фигура
. Говорят, что фигура 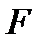 симметрична относительно прямой
симметрична относительно прямой 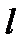 . [1, стр. 164-166]
. [1, стр. 164-166]
\
Метод симметрии
Применение осевой симметрии к решению задач на построение называют методом симметрии.
Суть: состоит в том, что на ряду с данными и искомыми фигурами рассматриваются также фигуры, симметричные некоторыми из них относительно некоторой оси. При удачном выборе оси и преобразуемой фигуры решение задачи может значительно облегчиться, а в иных случаях симметрия непосредственно дает искомые точки.
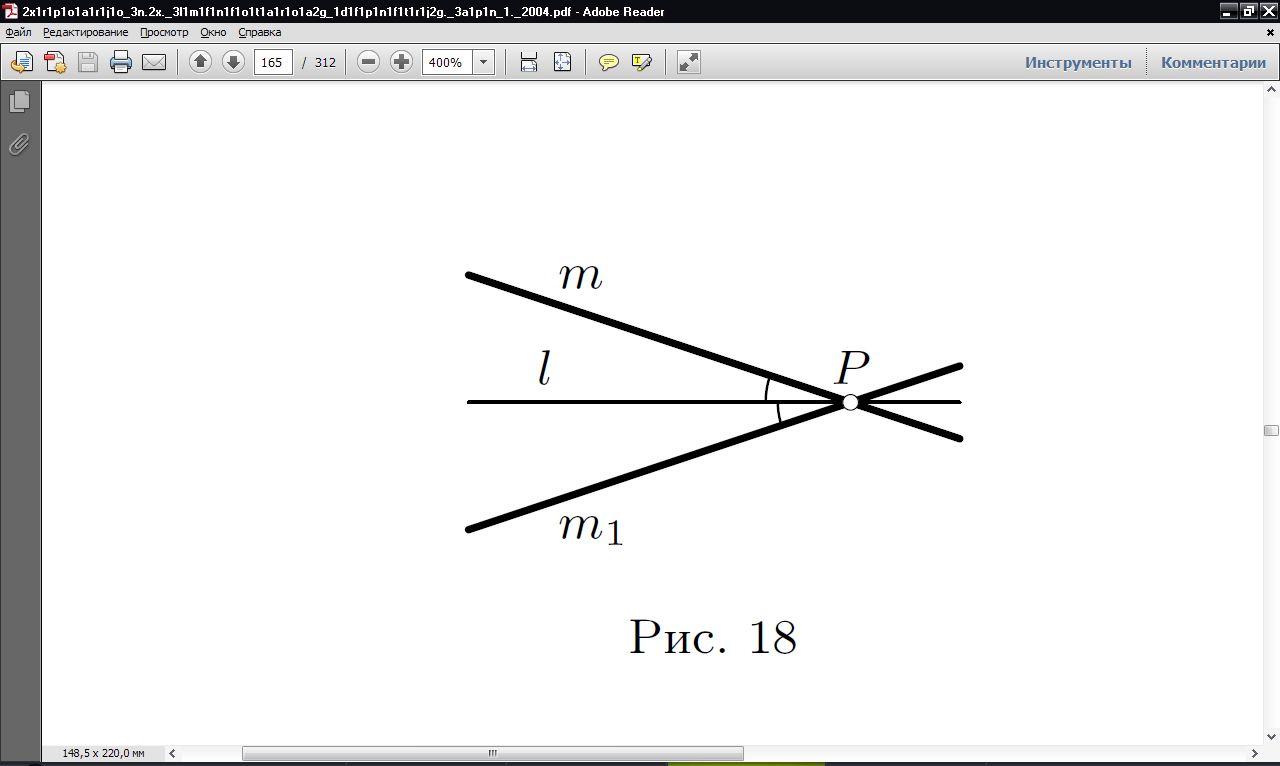
Задача 1. Отрезок 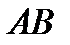 пересекает прямую
пересекает прямую 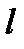 . Постройте на прямой
. Постройте на прямой 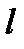 точку
точку 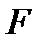 так, чтобы прямая
так, чтобы прямая 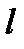 делила угол
делила угол 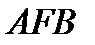 пополам.
пополам.
Задача 2.Построить квадрат, две противоположные вершины которого лежат на данной прямой 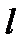 , а две другие – соответственно на данных окружностях
, а две другие – соответственно на данных окружностях 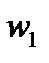 и
и 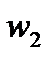 .
.
Задача 3. Построить ромб так, чтобы одна из его диагоналей была равна данному отрезку 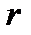 и лежала на данной прямой
и лежала на данной прямой 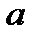 , а остальные две вершины ромба лежали соответственно на данных прямых
, а остальные две вершины ромба лежали соответственно на данных прямых 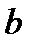 и
и  .
.
Задача 4.Постройте отрезок 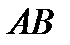 так, чтобы его концы принадлежали данным прямым
так, чтобы его концы принадлежали данным прямым 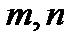 и так, чтобы данная прямая
и так, чтобы данная прямая 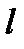 проходила через середину отрезка
проходила через середину отрезка 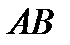 и была ему перпендикулярна.
и была ему перпендикулярна.
Задача 5. Построить треугольник, зная сторону 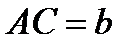 , прилежащий к ней угол
, прилежащий к ней угол 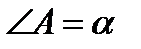 и разность двух других сторон
и разность двух других сторон 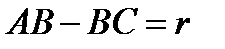 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|