
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
К стержню приложена сила F. Заменить ее двумя параллельными ей силами, приложенными к стержню в точках А и В (рис. 11.24). (FA = 2F; FB = -F)
11.84.К стержню приложена сила F. Заменить ее двумя параллельными ей силами, приложенными к стержню в точках А и В (рис. 11.24). (FA = 2F; FB = -F)
11.85.От однородного стержня отрезали кусок длиной 40 см. На сколько сместился центр тяжести стержня? (20 см)
11.86.На правом конце стержня длиной 30 см прикреплен шар радиусом 6 см. На каком расстоянии от левого конца стержня находится центр тяжести системы, если масса стержня вдвое меньше массы шара? (29 см)
11.87.
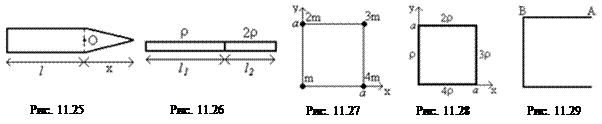 |
Какой должна быть высота x треугольной части тонкой однородной пластины, чтобы центр тяжести пластины находился в точке О? Длина прямоугольной части равна l (рис. 11.25). (
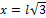 )
)
11.88.Стержень спаян из двух одинаковых по сечению стержней, изготовленных из материалов с плотностями r и 2r (рис. 11.26). При каком отношении длин стержней l1/l2 центр тяжести системы будет находиться в плоскости спая? ( 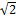 )
)
11.89.Из однородного диска радиусом R вырезано круглое отверстие радиусом r, центр которого находится на расстоянии ½ R от центра диска. На каком расстоянии от центра диска находится центр тяжести системы?
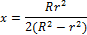
11.90.В квадратной пластинке со стороной 12 см вырезано круглое отверстие радиусом 3 см, касающееся двух смежных сторон квадрата. На каком расстоянии от центра квадрата находится центр тяжести пластинки? (1 см)
11.91.В вершинах квадрата со стороной а находятся точечные массы: m, 2m, 3m и 4m. С квадратом связана система координат (рис. 11.27). Найти координаты центра тяжести системы. (xc = 0,7a; yc = 0,5a)
11.92.Квадрат со стороной а составлен из четырех тонких стержней одинакового сечения, сделанных из разных материалов с плотностями: r, 2r, 3r и 4r. С квадратом связана система координат (рис. 11.28). Найти координаты центра тяжести системы. (xc = 0,6a; yc = 0,4a)
11.93.Тяжелый стержень согнут посередине под прямым углом и подвешен свободно за один из концов. Какой угол с вертикалью образует верхняя половина стержня? (»18,40)
11.94.Квадратная рамка изготовлена из однородной проволоки. У нее отрезали одну сторону (рис. 11.29). Найти угол между средней стороной и вертикалью, если рамку подвесить на нити за: а) вершину А; б) вершину В. (а) » 530; б) » 33,7º)
11.95.
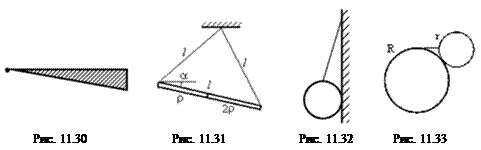 |
Из однородной пластины вырезан прямоугольный треугольник с острым углом 30º. Этот треугольник подвешен шарнирно за этот угол к потолку. Какую минимальную силу нужно приложить, чтобы удерживать его в положении, изображенном на рис. 11.30? Масса треугольника m.
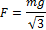
11.96.Стержень длиной l, составленный из двух половинок, висит на двух нитях длиной l. Какой угол составляет стержень с горизонтом в равновесии, если половинки изготовлены из материалов с плотностями r и 2r (рис. 11.31)? (» 5,5º)
11.97.Шар висит на нити у вертикальной стены так, что точка крепления нити к шару и центр шара находятся на одной вертикали (рис. 11.32). При каком коэффициенте трения это возможно? (³ 1)
11.98.На шаре радиусом R лежит шар массой m и радиусом r, привязанный нитью к большому шару в верхней его точке. Найти силу натяжения нити, если известно, что она горизонтальна (рис. 11.33). Трения нет.
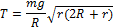
11.99. 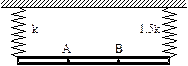 На горизонтальном столе лежит лист бумаги, прижатый однородным стержнем массой 0,5 кг, верхний конец которого шарнирно закреплен. Какую минимальную горизонтальную силу необходимо приложить к листу, чтобы вытащить его? Угол между стержнем и листом 60°, коэффициент трения между ними 0,3, трением между листом и столом пренебречь. (» 0,5 Н)
На горизонтальном столе лежит лист бумаги, прижатый однородным стержнем массой 0,5 кг, верхний конец которого шарнирно закреплен. Какую минимальную горизонтальную силу необходимо приложить к листу, чтобы вытащить его? Угол между стержнем и листом 60°, коэффициент трения между ними 0,3, трением между листом и столом пренебречь. (» 0,5 Н)
11.100.Горизонтальный невесомый стержень висит на двух вертикальных пружинах, жесткости которых равны k и 1,5k. Точки А и В делят длину стержня на три равные части. К точке А стержня подвешивают груз массой m. Груз какой массы надо подвесить в точке В, чтобы стержень остался горизонтальным? (mx = 4m)
11.101. 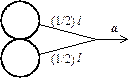 Две одинаковые шайбы массой m и радиусом R лежат, соприкасаясь, на гладкой горизонтальной поверхности и связаны нитью длиной l. За середину нити начинают тянуть с ускорением а. С какой силой шайбы давят друг на друга?
Две одинаковые шайбы массой m и радиусом R лежат, соприкасаясь, на гладкой горизонтальной поверхности и связаны нитью длиной l. За середину нити начинают тянуть с ускорением а. С какой силой шайбы давят друг на друга?
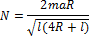
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|