Линия заданного пути на карте задается заданным путевым углом (ЗПУ).

Линия заданного пути на карте задается заданным путевым углом (ЗПУ).

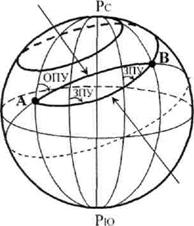
Ортодромический путевой угол (ОПУ) - угол, заключенный между северным направлением меридиана начальной точки ортодромии и ЛЗП.

Полет по ортодромии может быть выполнен только с помощью ортодромических курсовых систем (приборов).

Ортодромия

Локсодромия

Рис. 1.7. Ортодромия и локсодромия

Экватор и меридианы можно рассматривать как частные случаи ортодромии. На картах ортодромия между двумя пунктами, расположенными на расстоянии 1000 -1200 км, практически изображается прямой линией.

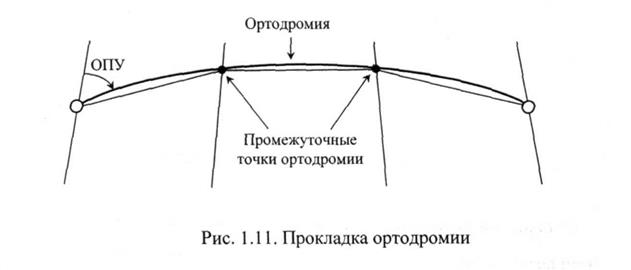
На больших расстояниях ортодромия имеет вид кривой линии, обращенной выпуклостью к полюсу (рис. 1.7). В этом случае ее прокладывают по промежуточным точкам. Долготы промежуточных точек можно брать произвольно, но для удобства расчета их обычно берут через 10 - 20°.

Локсодромия— линия на поверхности земного шара между двумя точками (А и В), пересекающая меридианы под постоянным путевым углом (рис. 1.7). Локсодромия представляет собой логарифмическую спираль, которая огибает земной шар бесконечное число раз и стремится к полюсу, но никогда не достигает его. Своей выпуклостью она обращена всегда к экватору.

Такой вид локсодромии объясняется тем, что ее путевой угол, относительно каждого меридиана, остается постоянным, а сами меридианы не параллельны друг другу, а сходятся к полюсам (рис. 1.12).

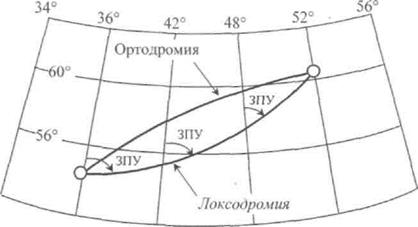
Рис. 1.12. Вид ортодромии и локсодромии на карте.

Локсодромический путевой угол- постоянный угол, под которым локсодромия пересекает меридианы (рис. 1.12). Путь по локсодромии длиннее пути по ортодромии, кроме частных случаев, когда она совпадает с экватором или меридианами, которые являются одновременно и ортодромией и локсодромией.

В практике аэронавигации полеты по локсодромии выполняют, как правило, на воздушных судах 4-го класса и вертолетах всех классов с помощью магнитного компаса или курсовой системы в режиме «МК».

Маршрут полета не является прямой от пункта вылета до пункта посадки, а имеет ряд изломов. Длину участка маршрута выбирают такой, чтобы разность путевых углов в начале и в конце участка не превышала 2°.

При этом условии ЛЗП на полетной карте прокладывается в виде прямой, которую принимают за локсодромию.

При расстоянии между точками на земной поверхности до 250 км локсодромия незначительно отклоняется от прямой линии, т.е. практически совпадает с ЛЗП.

Локсодромический путевой угол участка маршрута измеряют непосредственно на карте транспортиром относительно меридиана средней точки данного участка (рис. 1.13). Длину пути по локсодромии измеряют на карте с помощью масштабной или сантиметровой линейки.

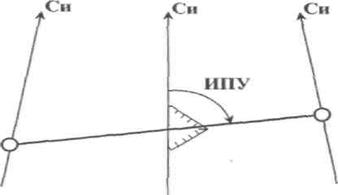
Средний меридиан участка

6. Системы координат.

Для определения положения точки (объекта, воздушного судна) на поверхности Земли или некоторой точки над земной поверхностью необходима система координат.

В практике аэронавигации наиболее широко используются следующие системы координат: географическая, сферическая, ортодромическая, полярная.

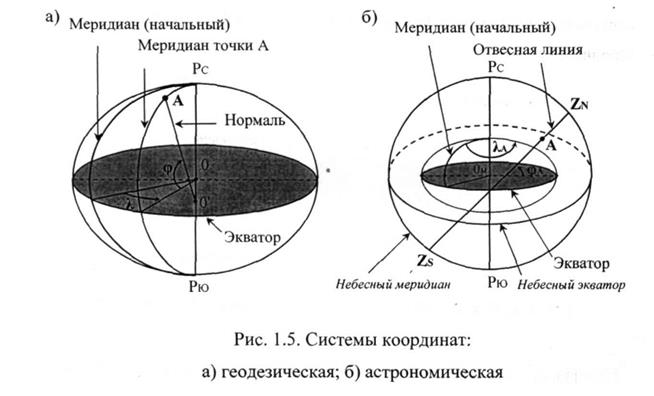
Географическая система координат.Строго говоря, такой системы координат нет. Этот термин объединяет две системы координат: геодезическую и астрономическую (рис. 1.5).

Так, для определения положения точки на поверхности земного эллипсоида применяют геодезическую систему координат, а для определения положения точки на поверхности геоида (Земли) соответственно астрономическую.

Отличие состоит лишь только в том, что астрономическую широту отсчитывают до отвесной линии в данной точке геоида (рис. 1.5, б), а геодезическую широту - до нормали к поверхности эллипсоида в данной точке (рис. 1.5, а) .

Для приближенного решения задач, когда не нужно учитывать разности геодезических и астрономических координат точек, применяются географические координаты, в качестве которых используется геодезическая широта и долгота.

Принято, геодезические координаты называть географическими.

Географическая (геодезическая) широта j - угол, заключенный между плоскостью экватора и нормалью к поверхности земного эллипсоида в данной точке А. Широта измеряется от экватора в сторону полюсов от 0 до 90° и называется, соответственно, северной (положительной) и южной (отрицательной).

Поскольку нормаль к поверхности эллипсоида не проходит через центр О, широту нельзя измерять центральным углом. Ее нельзя измерять и дугой меридиана, так как кривизна последнего является переменной величиной.

Географическая (геодезическая) долгота l - двугранный угол, заключенный между плоскостями начального меридиана и меридиана данной точки А. Долгота измеряется от начального меридиана к востоку и западу от 0 до 180° и называется соответственно

восточной (положительной) и западной (отрицательной).

Долгота, кроме угловых величин, может измеряться в единицах времени, необходимого Земле для того, чтобы повернуться вокруг своей оси на угол, который соответствует дуге, измеряющей долготу. При этом считают, что каждые 15° долготы соответствует 1 ч времени.

⇐ Предыдущая 1 234 Следующая ⇒