
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Интегральный расчет функции одной переменной
@@@ Интегральный расчет функции одной переменной
$$$
A. 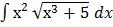 вычислить неопределенный интеграл.
вычислить неопределенный интеграл.
A. 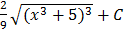
B. 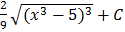
C. 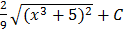
D. 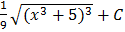
E. нет правильного ответа
$$$
Вычислить интеграл 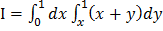
A. 1
B. -1/2
C. 1/2
D. 0
E. нет правильного ответа
$$$
Сколько свойств имеет неопределенный интеграл?
A. 5
B. 8
C. 6
D. 3
E. 7
$$$
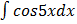 вычислите неопределенный интеграл.
вычислите неопределенный интеграл.
A. 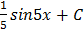
B. 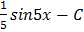
C. 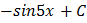
D. 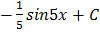
E. 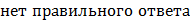
$$$
Найди формулу интегрирования по частям?
A. 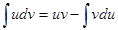
B. 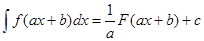
C. 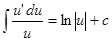
D. 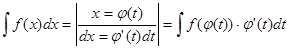
E. 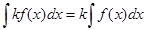
$$$
Какая формула называется формулой подстановки интегрирующей переменной определенного интеграла?
A. 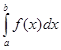
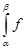 j(α)
j(α) 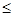 j(t)dt
j(t)dt
B. 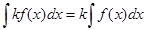
C. 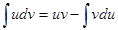
D. 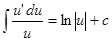
E. нет правильного ответа
$$$
Вычислить неопределенный интеграл 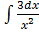 .
.
A. 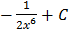
B. 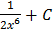
C. 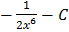
D. 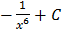
E. 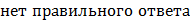
$$$
Вычислить интеграл 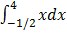
A. 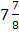
B. 
C. 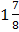
D. 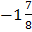
E. 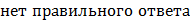
$$$
Вычислить интеграл 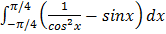
A. 2
B. 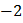
C. 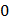
D. 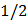
E. 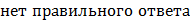
$$$
Вычислить интеграл 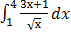 .
.
A. 16
B. 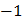 6
6
C. 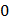
D. 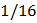
E. 
$$$
Вычислить интеграл 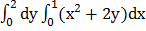
A. 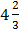
B. 
C. - 
D. 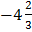
E. нет правильного ответа
$$$
Значение повторного интеграла 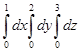 , равно…
, равно…
A. 6
B. 4
C. 3
D. 1
E. 0
$$$
Вычислить двойной интеграл: 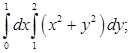
A. 3
B. -7/3
C. 2
D. 5/3
E. 6
$$$
Вычислить двойной интеграл: 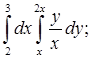
A. 15/4
B. 4
C. 15/2
D. 7
E. 13/6
$$$
на отрезке [a,b] функция f(x) непрерывна,а на отрезке [αβ] функция (t) и ее производная являются частным и непрерывными (при a 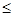 t
t 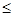 b функция a=j(α)
b функция a=j(α) 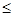 j будет (t)
j будет (t) 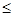 j(β) = b Как называется этот метод?
j(β) = b Как называется этот метод?
A. Метод замены переменную интегрирования
B. Метод прерывания
C. Метод интеграла Римана
D. Метод частичного интегрирования
E. Метод определенного интеграла
$$$
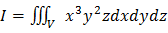 , V зона 0≤x ≤1, 0 ≤y ≤x, 0 ≤z ≤xy.
, V зона 0≤x ≤1, 0 ≤y ≤x, 0 ≤z ≤xy.
A. 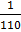
B. 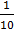
C. 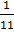
D. 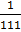
E. нет правильного ответа
$$$
предположим, что функции и производные u = u(x), v = v(x) находятся на отрезке [a, b], к какому методу это относится?
A. Метод интегрирования по частям
B. Метод прерывания
C. Создайте переменную интегрирования метод замены
D. Метод интеграла Римана
E. Метод определенного интеграла
$$$
найти общий Интеграл уравнения 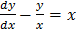
A. 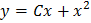
B. 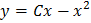
C. 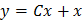
D. 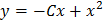
E. нет правильного ответа
$$$
Покажи формулу Ньютон-Лейбница?
A. 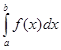 = F(b)-F(a)
= F(b)-F(a)
B. 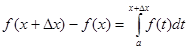
C. C. 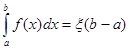
D. 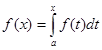 a
a 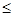 x
x 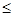 b
b
E. 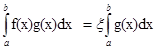
$$$
Значение повторного интеграла 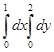 , равно
, равно
A. 2
B. 1
C. - 2
D. 0
E. 3
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|