Размещения. Сочетания

Размещения

Размещение –это набор изmразличных элементов некоторого n-элементного множества, причем два размещения, отличающиеся порядком следования элементов, считаются различными. Стандартным обозначением для числа размещений m элементов из n является символ 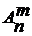. Число размещений вычисляется по формуле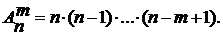

Эту формулу можно переписать в виде .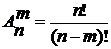

Рассмотрим небольшую модификацию предыдущей задачи.

Задача 4. Десять участников полуфинала разыгрывают три путевки в финал. Сколько существует вариантов формирования тройки финалистов?

Решение.Ответ предыдущей задачи придется отвергнуть. Действительно, тройки финалистов, отличающиеся порядком следования участников (например, Иванов, Петров, Сидоров и Петров, Иванов, Сидоров), следует считать одинаковыми. Фактически, ответ предыдущей задачи следует разделить на число возможных перестановок призеров, равное 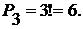Таким образом, число вариантов равно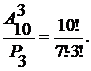

Теперь мы можем перейти к одному из наиболее важных понятий комбинаторики.

Сочетания

Сочетание–это набор изmразличных элементов некоторого n-элементного множества, причем два любых сочетания, отличающиеся порядком следования элементов, совпадают. Стандартным обозначением для числа сочетаний m элементов из nявляется символ 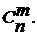Число сочетаний вычисляется по формуле .

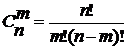В задачах комбинаторики числа 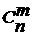часто называют биномиальными коэффициентами. Это связано с тем, что они выступают в качестве коэффициентов в формуле бинома Ньютона

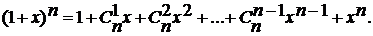
Между биномиальными коэффициентами имеется много важных и интересных соотношений. Например, 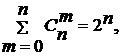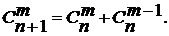. Последнее тождество позволяет быстро вычислять биномиальные коэффициенты для небольшихn по следующему правилу: для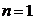 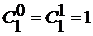и формула позволяет перейти к 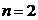и т.д. Для использования этого алгоритма надо помнить, что 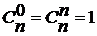при любом n.

⇐ Предыдущая 1 234 Следующая ⇒