КОМБИНАТОРНЫЕ ФОРМУЛЫ. Правило произведения

КОМБИНАТОРНЫЕ ФОРМУЛЫ

В этом разделе мы приведем ряд комбинаторных формул, часто используемых при решении вероятностных задач. Начнем с решения одной простой задачи.

Задача 1 .Обед в университетской столовой состоит из трех блюд. Первых блюд в меню 5, вторых блюд – 4, а третьих -- 3. Сколько дней студент может съедать новый обед, если любая комбинация блюд возможна, и один обед от другого должен отличаться хотя бы одним блюдом?

Решение. «Закодируем» обед трехзначным числом 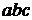, где 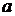-- номер первого блюда ( 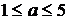), 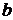-- номер второго блюда ( 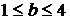) 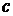-номер третьего блюда ( 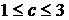). При любом фиксированном a параметр b может принимать 4 различных значения. Поскольку сам параметр a может принимать 5 различных значений, то имеется 5∙4=20 различных пар ab. С другой стороны, при каждой фиксированной паре ab параметр c может принимать 3 различных значения. Поэтому количество различных троек 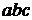равно 20∙3=60. Таким образом, число различных обедов равно 60.

Алгоритм решения задачи легко поддается обобщению и позволяет получить следующее правило.

Правило произведения

Обозначим через 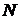число способов, которыми можно заполнить строчку 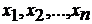, если для выбора элемента 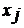существует 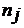вариантов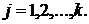

Тогда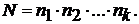

Это правило иногда используется, когда речь идет о выборах элементов из заданного множества, причем, выбор происходит без возвращения. В этом случае 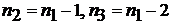и так далее. Рассмотрим пример такой ситуации.

Задача 2 Вам надо позвонить пятерым своим друзьям. Сколько имеется способов выстроить очередность этих звонков?

Решение. Первый Ваш звонок может быть адресован любому из Ваших 5 друзей, второй – любому из 4 оставшихся друзей, которым Вы еще не позвонили и т. д. Поэтому задача решается с помощью приведенной выше формулы при 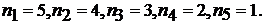Ответ 120 способов.

Решение этой задачи подводит нас к следующему определению.

12 3 4 Следующая ⇒