Задача № 3

Задача № 3

Для заданной схемы требуется подобрать стальную двутавровую балку.

Дано: а=2,2м, в=3,4м, с=1,9м, L=10,0м, М=7кНм, F=19kH,

q=21кН/м.

Решение:

1). Определяем реакции в опорах А и В из ур-й равновесия балки. Составим ΣМ_А=0.

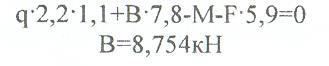
Составим: ΣМв⁼0

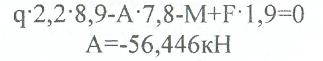
Проверяем правильность определения реакции:

A-q-2,2-F+B=0

56,446-46,2-19+8,754=0

Балка имеет четыре характерных участка, составим для них уравнения для определения поперечной Q силы и изгибающего момента М

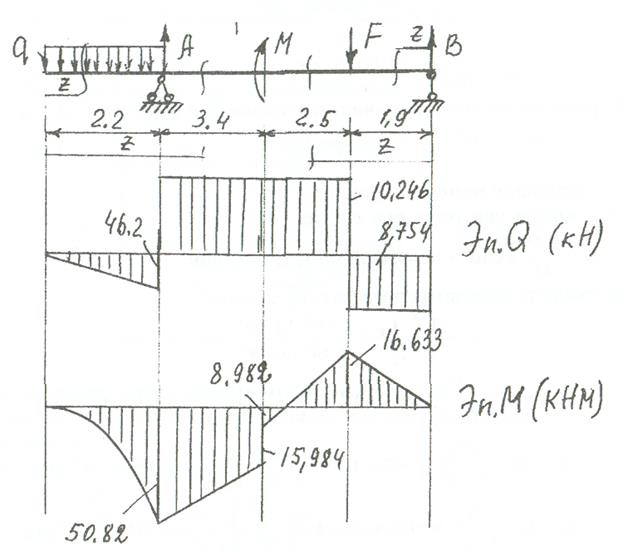
Q₁=-qz; 0 <z<2,2;

Q₂=-q-2,2+A; 2,2:Ј<S,6;

M₂=-q-2,2(z-l,l)+A-(z-2,2);

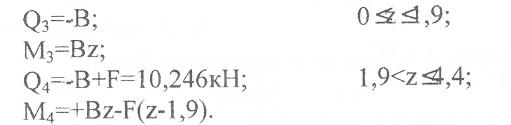
Q₃=-B; 0<£<1,9;

M₃-Bz;

Q₄=-B+F=10,246kH; 1,9<z^,4;

M,=+Bz-F(z-1,9).

После подстановки значений z полученные величины откладываем на эпюре «М», «Q».

Опасное сечение на левой опоре М_m_ах=50,82кНм. Для подбора двутавровой балки воспользуемся условием прочности (1).

Где [σ]=15кН/см из него находим момент сопротивления:

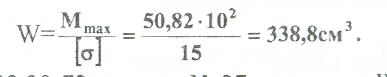
Выбираем по ГОСТ 82 39-72 двутавр № 27 имеющим W=371 см'. Определяем напряжение в нём (1).

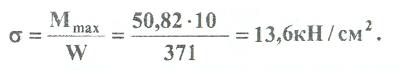
Отклонение 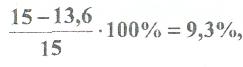что допустимо.